Особенности турбулентного течения

ЛЕКЦИЯ 15.

Опыт показывает, что если числа Re превосходят некоторый предел, то ламинарное течение становится невозможным и возникает другой тип течения, которое называют турбулентным. Систематические исследования в этом направлении начались с известного опыта Рейнольдса (1883 г.).

Если в трубу с прозрачными стенками, по которой движется жидкость, пустить струйку краски, то окрашенная струйка при ламинарном течении будет двигаться вдоль трубы, почти не размываясь. Скорость поперек трубы при этом, как предсказывает теория, меняется по параболическому закону (рис. 6.3, а).

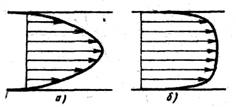Рис.6.3. Распределение скорости в трубе: а – ламинарное течение; б – турбулентное течение

При увеличении расхода жидкости через трубу увеличивается скорость и, следовательно, число Re. При некотором числе Re характер движения жидкости в трубе изменяется. Струйка краски начнет испытывать поперечные пульсации, размоется и окрасит весь поток. При этом распре-

деление средней по времени скорости в поперечном сечении трубы станет более полным (рис. 6.3, б). Изменение эпюры скорости указывает на то, что изменился и закон трения, так как ламинарному закону трения соответствует параболическое распределение скорости.

В связи с этим коэффициент Кориолиса α, учитывающий неравномерность распределения кинетической энергии по сечению в уравнении Д.Бернулли, при турбулентном течении значительно меньше, нежели при ламинарном: он является функцией числа Re, уменьшаясь с увеличением последнего от 1,13 при Re = Re_кр до 1,025 при Re = 3·10⁶. В инженерной практике значение α принимают равным 1.

Аналогичная картина может наблюдаться и в пограничном слое, например, на плоской пластине. Сначала окрашенная струйка движется в пограничном слое вдоль пластины, не размываясь. На некотором расстоянии в струйке возникнут усиливающиеся поперечные пульсации и краска размоется. При возникновении пульсаций эпюра скоростей в поперечном сечении пограничного слоя также изменяется, становится более полной, т. е. не соответствует закону трения при ламинарном течении.

Таким образом, опыт показывает, что в вязкой жидкости возможны две формы течения: ламинарная, когда жидкость движется слоями, и турбулентная, когда в потоке возникают малые хаотические пульсации скорости и давления вокруг средних значений этих величин. При турбулентном течении наряду с основным продольным перемещением жидкости вдоль трубы имеют место поперечные перемещения и вращательное движение отдельных объемов жидкости.

В действительности ламинарные течения наблюдаются только при доста-точно малых числах Re. Это объясняется тем, что при больших числах Re лами-нарные течения теряют устойчивость и переходят в турбулентные. Опыты пока-зывают, что ламинарное течение в круглой трубе существует, если Re < 2300. Однако эта граница довольно условна, так как устойчивость ламинарного течения зависит также от возмущений потока на входе в трубу. Весьма тщательным устранением источников возмущений удалось, например, добиться ламинарного течения в трубе для Re ≈ 40 000. С другой стороны, следует отметить, что, сколь бы сильными не были возмущения на входе, они гаснут, и поток в трубе остается ламинарным, если Re < 2300.

Большое практическое значение имеет вопрос об устойчивости лами-нарного пограничного слоя. Все причины, которые могут вызвать пульсации в ламинарном пограничном слое, понижают его устойчивость, т.е. вызывают его переход в турбулентный при меньших числах Re. Устойчивость ламинарного пограничного слоя понижается при увеличении пульсаций во внешнем потоке, увеличении положительного градиента давления, увеличении шероховатости стенки.

Основной особенностью турбулентного течения является хаотическая пульсация скорости и давления в любой фиксированной точке пространства. Пульсации вызываются быстрым и хаотическим перемещением и перемешива-нием элементарных частиц жидкости. Эти малые пульсации накладываются на основное установившееся течение жидкости. Хотя пульсации весьма малы по сравнению со скоростью основного потока, они, как показал Рейнольдс, приводят к появлению турбулентного трения, которое существенно больше трения при ламинарном движении.

Поскольку теоретическое изучение турбулентных течений с хаотическими пульсациями встречает непреодолимые трудности, в большинстве случаев для практических расчетов, связанных с турбулентным течением жидкостей в трубах прибегают к экспериментальным данным.

Основной расчетной формулой для турбулентного течения в круглых трубах является формула Дарси:

или

где λ – коэффициент путевых потерь при турбулентном режиме течения, в общем случае зависящий от числа Рейнольдса и от шероховатости омываемой поверхности.

Опыты по изучению движения жидкости в шероховатых трубах показали:

1. При ламинарном режиме шероховатость на сопротивление не влияет, коэффициент путевых потерь вычисляется по формуле Пуазейля:

.

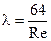2. Критическое число Re от шероховатости практически не зависит.

3. В области турбулентного течения, но при небольших значениях числа Re и относительной шероховатости шероховатость на сопротивление не влияет; коэффициент потерь можно вычислять либо по формуле Блазиуса

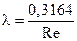
в диапазоне чисел Re 4000 < Re < 10⁵, либо по формуле П.К. Конакова

λ = (1,81·lgRe – 1,5)^-2

при любом Re > 4000.

4. При больших значениях числа Re и больших относительных шероховатостях коэффициент путевых потерь перестает зависеть от числа Re и делается постоянным для данной относительной шероховатости. Этот режим турбулентного течения называют режимом квадратичного сопротивления, так как независимость коэффициента путевых потерь λ от числа Re делает потерю давления (напора) пропорциональной точно квадрату скорости. На рис.64. представлены зависимости коэффициента путевых потерь от числа Re для разных значений d/k_э, где k_э – абсолютная эквивалентная шероховатость, d – диаметр трубы. Штриховая линия указывает значения чисел Re, начиная с которых течение становится автомодельным, т.е. не зависящим от числа Re.

Рис. 6.4.Зависимость коэффициента путевых потерь для шероховатых труб

Для инженерных расчетов коэффициент путевых потерь для круглых труб с неравномерной шероховатостью стенок можно вычислять по формуле Альтшуля:

или, когда число Re очень велико, по формуле Шифринсона .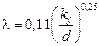

Дата добавления: 2014-01-11