
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Конспект лекций. Задача. Расчет глубины центральной воронки в сосуде с мешалкой
|
|
|
|
Задача. Расчет глубины центральной воронки в сосуде с мешалкой.
Найти глубину центральной воронки при стационарном движении жидкости в большом резервуаре без отражательных перегородок (рис. 5.6), заполненном маслом, как функцию скорости мешалки. Сделать это предполагается путем проведения модельных опытов в геометрически подобном сосуде меньших размеров. Поэтому определим условия, при которых следует осуществлять модельные испытания, чтобы обеспечить правильный способ предсказания результатов.
Решение. Структура потоков в аппарате настолько сложна, что не допускает выполнения точных расчетов. Следовательно, нужно использовать методы теории подобия и анализа размерностей. Форма центральной воронки для любого сосуда с мешалкой будет одна и та же при одинаковых безразмерных дифференциальных уравнениях и безразмерных граничных условиях, описывающих течение. Очевидно, что эти дифференциальные уравнения суть уравнения неразрывности и движения. Граничные условия следующие:
| Большой аппарат u =0 при z= 0 в области 0 < r < T 1/2 u =0 при r= T1/2 в области 0< z<H1 p=p0 на S1(r,z) | Малый аппарат u =0 при z= 0 в области 0 < r < T 2/2 u =0 при r= T2/2 в области 0< z<H2 p=p0 на S2(r,z) |
3десь S1 и S2 — поверхности воронки в большом и малом сосудах; р0 — атмосферное давление.
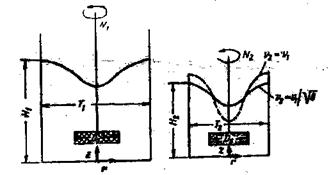
Рис. 5.6. Центральная воронка в сосуде с мешалкой
Можно также написать, что скорость относительно всех движущихся твер-дых поверхностей на этих поверхностях равна нулю. Однако указанных выше граничных условий достаточно, чтобы наглядно показать метод, который мы собираемся применить. В дальнейшем предположим, что процесс протекает стационарно, и, следовательно, отпадает необходимость в начальных условиях. В качестве характерного линейного размера выберем диаметр турбинной мешалки D, а в качестве характерного значения скорости — величину DN, равную произведению диаметра мешалки на скорость ее вращения в оборотах в единицу времени. Числа Рейнольдса и Фруда в данном случае принимают соответственно вид [ D2Nρ/μ ] и [ DN2/g ]. Тогда граничные условия, выраженные в новых без-размерных переменных, запишутся так:
Большой аппарат
  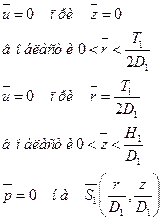
| Малый аппарат
 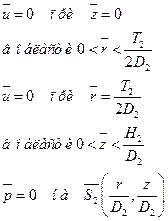
|
Теперь нетрудно убедиться, что для того, чтобы картины течения в двух сосудах с мешалками были подобны, должны выполняться следующие соотношения:


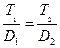 (7.3)
(7.3)
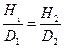 (7.4)
(7.4)
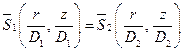 (7.5)
(7.5)
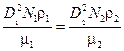 (7.6)
(7.6)
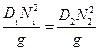 (7.7)
(7.7)
Уравнения (7.3) и (7.4) характеризуют условия геометрического подобия. Очевидно, что чем детальнее описание поверхности с нулевой скоростью, тем больше мы должны иметь таких геометрических соотношений. На практике могут оказаться существенными даже относительная шероховатость внутренних поверхностей резервуара и размеры головок болтов. Соотношение (7.5), вероятно, может быть удовлетворено, если форма центральных воронок одинакова, так как 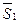 (r/D1 z/D1 и
(r/D1 z/D1 и 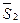 (r/D2, z/D2) - форма воронок, записанная в безразмерных координатах.
(r/D2, z/D2) - форма воронок, записанная в безразмерных координатах.
Уравнения (7.6) и (7.7) устанавливают требуемые соотношения между масштабными коэффициентами и, с нашей точки зрения, представляют наиболь-ший интерес. Поскольку на практике трудно менять гравитационное поле, из уравнения (7.7) следует, что
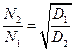 (7.8)
(7.8)
Подставляя это выражение в уравнение (7.6), получим:
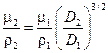
Мы подошли, наконец, к весьма любопытному результату, что динамическое подобие (для данного примера подобие центральных воронок) не может быть достигнуто в случае использования в обоих сосудах одной и той же жидкости. Предпочтительно, чтобы в меньшем сосуде применялась менее вязкая жидкость. При линейных размерах малого аппарата, составляющих половину соответствующих размеров большого аппарата, кинематическая вязкость в нем должна отвечать значению кинематической вязкости масла в большом аппарате, умноженному на 1/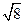 .
.
Контрольные вопросы
1. Какова необходимость моделирования в гидравлике?
2. Дать формулировку подобия физических явлений
3. Каково необходимое условие подобия физических явлений?
4. Что такое моделирование?
5. Описать процедуру выявления критериев подобия для течения несжимаемой жидкости.
6. Каков физический смысл критерия Рейнольдса? Записать для него выражение.
7. Каков физический смысл критерия Фруда? Записать для него выражение.
8. Какие требования предъявляются к начальным и граничным условиям при моделировании явлений?
9. Для задачи перемешивание несжимаемой жидкости мешалкой записать условия геометрического подобия.
10. Для задачи перемешивание несжимаемой жидкости мешалкой записать условия динамического подобия.
11. Какое условие должно быть выполнено, если в задаче о перемешивании жидкости выполняются условия геометрического и динамического подобия?
ЛИТЕРАТУРА
Основная
1. Шейпак А.А. Гидравлика и гидропнемопривод: Учебное пособие.Ч.1. Основы механики жидкости и газа. 2-е изд., перераб. и доп. – М.:МГИУ. 2003. – 192 с.
2. Сергель О.С. Прикладная гидрогазодинамика: Учебник для авиационных вузов. – М.: Машиностроение, 1981. – 374 с.
3. Самойлович Г.С. Гидрогазодинамика: Учебник для студентов вузов, обучающихся по специальности «Турбостроение». – 2-е изд., перераб. и доп. – М.: Машиностроение, 1990. – 384с.
Дополнительная
1. Берд Р.,Стьюард В. Лайтфут Е. Явления переноса. – М.: Химия, 1974. – 688 с.
2. Матвеев А.Н. Молекулярная физика: Учеб. пособие для вузов. – М.: Высшая школа, 1981. – 400 с.
СОДЕРЖАНИЕ
ЛЕКЦИЯ 1 2
1. ВВЕДЕНИЕ 2
1.1. Предмет гидравлики и ее место в технике. 2
1.2. Методика решения задач в гидравлике. 2
1.3. Основные понятия о процессах переноса. 4
1.4. Молекулярный перенос. 6
1.4.1. Основные положения молекулярно-кинетической теории газов. 6
1.4.2 Общее уравнение переноса. 6
1.4.3. Перенос тепла - теплопроводность. 7
ЛЕКЦИЯ 2 10
1.4.4. Перенос импульса - вязкость. 10
1.4.5. Самодиффузия. 13
ЛЕКЦИЯ 3 16
2. Основные физические характеристики жидкостей и газов. 16
2.1. Жидкости и газы. Гипотеза сплошности. 16
2.2. Параметры состояния. 19
2.3. Вязкость. 22
2.4. Модели жидкости. 25
ЛЕКЦИЯ 4 27
3. ГИДРОСТАТИКА 27
3.1. Силы, действующие в жидкости. 27
3.2. Свойство гидростатического давления. Основной закон гидростатики. 28
3.3. Закон Архимеда. 33
ЛЕКЦИЯ 5. 38
4. ОСНОВНЫЕ УРАВНЕНИЯ МЕХАНИКИ ЖИДКОСТИ И ГАЗА 38
4.1. Некоторые понятия в МЖГ. 38
4.3. Использование буквенных индексов. 40
4.4 Методика решения задач в МЖГ. 44
ЛЕКЦИЯ 6 47
4.5 Уравнение неразрывности. 47
4.6 Уравнение движения. 51
ЛЕКЦИЯ 7 54
4.7. Уравнение моментов количества движения (второе уравнение Эйлера) 56
4.8 Уравнение энергии. 58
4.9 Уравнение механической энергии. 59
ЛЕКЦИЯ 8 62
4.10 Уравнение переноса тепловой энергии. 62
4.11. Теорема Коши-Гельмгольца. 63
4.12. Уравнение Навье – Стокса. 65
ЛЕКЦИЯ 9 69
5. ОДНОМЕРНОЕ ДВИЖЕНИЕ ЖИДКОСТИ 69
5.1. Уравнение неразрывности. 69
5.2 Уравнение движения. 70
5.3 Уравнение энергии. 71
5.4 Частные случаи уравнения энергии для одномерного потока. 73
5.4.1. Адиабатное течение газа. 73
5.4.2. Несжимаемая жидкость. 73
5.4.3. Невесомый идеальный газ. 75
ЛЕКЦИЯ 10 78
5.5 Характерные скорости в газовом потоке. 78
5.6. Безразмерные скорости. 79
5.7. Газодинамические функции параметров торможения. 81
5.8. Газодинамические функции расхода. 83
ЛЕКЦИЯ 11 87
5.9. Геометрическое воздействие на газовый поток. 87
5.10. Расходное воздействие на газовый поток. 88
5.11. Газодинамические функции полного потока импульса. 90
ЛЕКЦИЯ 12 95
5.12 Течение вязкой несжимаемой жидкости в трубах. 95
5.13. Течение вязкого газа в трубах. 97
5.14. Течение газа с теплоподводом.(тепловое воздействие на газовый поток) 100
ЛЕКЦИЯ 13 104
5.15 Механическое воздействие на газовый поток. 104
5.16. Движение вязкой жидкости с продольным градиентом давления. 107
ЛЕКЦИЯ 14 116
6. Примеры решения задач гидравлики 116
6.1. Ламинарное течение в круглых трубах. 116
ЛЕКЦИЯ 15. 122
6.2. Особенности турбулентного течения. 122
6.3. Струйные течения. 126
6.3.1. Свободная турбулентность. Турбулентные следы и струи. 126
ЛЕКЦИЯ 16 128
6.3.2. Круглая затопленная струя. 128
6.3.3. Плоская свободная струя. 133
ЛЕКЦИЯ 17 136
7. Физическое подобие. Моделирование 136
7.1. Общие положения. 136
7.2. Критерии подобия. 138
7.3. Задача. Расчет глубины центральной воронки в сосуде с мешалкой. 140
ЛИТЕРАТУРА 145
по дисциплине «Основы организации производства и менеджмент» для студентов специальностей «Теплоэнергетика» и «Промышленная теплотехника»
Утверждено
на заседании кафедры
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 624; Нарушение авторских прав?; Мы поможем в написании вашей работы!