Критерии подобия

Для многих гидродинамических систем могут быть выбраны характерные:

· линейный размер D;

· скорость U;

· разность температур;

· давление.

Выбор характерных величин достаточно произволен, но должен быть строго оговорен. После выбора характерных величин определяются соответствующие безразмерные переменные: 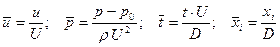. Запишем уравнения законов сохранения для несжимаемой жидкости в безразмерном виде. Для этого сначала выпишем для рассматриваемого случая уравнения в размерном виде:

В эти уравнения подставляем величины, выраженные через безразмерные переменные. Получаем

Умножаем уравнение неразрывности на D/U, уравнение движения на D/rU²:

Получившиеся уравнения безразмерны. Масштабные коэффициенты, описывающие размеры, скорость и физические свойства жидкости сконцентрировались в двух безразмерных группах:

- число Рейнольдса, определяющее соотношение массовых сил к вязким силам, и - число Фруда, определяющее соотношение массовых сил и силы веса.

Уравнение энергии в безразмерных переменных выглядит следующим образом:

.

В этом уравнении

F_u – диссипативная функция в безразмерных переменных;

Pr=c_pm/l - число Прандтля, характеризующее соотношение молекулярного процесса переноса количества движения и тепла;

Br=mU²/l(T₁-T₀) -число Бринкмана, характеризующее соотношение между тепловыделением за счет вязкости и теплопередачей теплопроводностью. Малые значения числа Бринкмана означают, что вязкое тепловыделение может быть выведено из объема теплопроводностью.

Произведение критериев Прандтля и Рейнольдса называют критерием Пекле: Pr×Re=Pe. Он может быть вычислен так: Pe=UD/a, где a - есть коэффициент температуропроводности.

Если в двух газодинамических системах критерии имеют одно и то же значение, то обе системы описываются одинаковыми дифференциальными уравнениями в безразмерных переменных. Если, кроме того, записанные в безразмерных величинах начальные и граничные условия одинаковы (это возможно при рассмотрении геометрически подобных систем), то эти две системы с точки зрения математического описания идентичны. Другими словами, поля безразмерных скоростей, давлений и других обезразмеренных величин одинаковы для каждой из изучаемых систем. Такие системы подобны в динамическом и энергетическом смыслах.

Дата добавления: 2014-01-11