Математическая постановка задачи управления

Как было сказано ранее, что для обеспечения нормального функционирования производства нужны, в общем случае, 8 подсистем управления. В зависимости от конкретной ситуации та или иная посистема имеет дело с различными постановками задач управления. Допустим, в одном случае, для одного производства, подсистема замены и ремонта оборудования решает задачу нахождения экстремума функции одной переменной, в другом, для другого производства – такая же подсистема решает задачу линейного или нелинейного программирования.

Можно, однако, все многообразие задач решаемых подсистемой управления свести к довольно ограниченному кругу типовых задач управления. Отметим следующие 6 типов задач, охватывающих большинство из практически встречающихся задач управления производством, за исключение задач стохастического и щелоченного применения и задач массового обслуживания.

1. Нахождение экстремума функции одной переменной без ограничений.

Постановка задачи. Найти extr f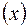 на открытом интервале (а, в) изменение аргумента (Унимодальная функция).

2. Нахождение экстремума функции одной переменной с ограничениями.

Постановка задачи. Найти extr f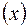 на замкнутом (т.е. включая граничные точки) отрезке [а, в] изменения аргумента х, включая и граничные точки.

3. Нахождение экстремума функции многих переменных без ограничений.

Постановка задачи. Найти extr f 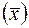, где 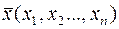, на открытом множестве 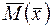. Иными словами на векторный аргумент 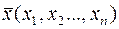не накладывается никаких ограничений.

4. Нахождение экстремума функции многих переменных с ограничениями.

Постановка задачи. Найти extr функции f 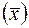, где 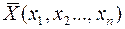, на замкнутом множестве 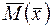. Замкнутое множество 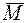обычно задается системой управлений или неравенств, связывающих аргументы .

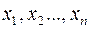Эта задача 4 разбивается на ряд частных задач.

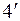Классическая зада Лагранжа.

Постановка задачи. Найти extr функции f 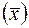на замкнутом множестве , т.е. на ограничениях типа равенств (иными словами, ограничения здесь суть управления).

Здесь 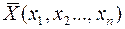- мерный вектор аргументов.

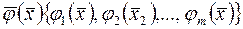m – мерная векторная функция, т.е. m- управлений ограничений (иногда говорят управлений связи). Класс задача Лагранжа имеет аналитическое решение.

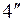Нахождение extr функций многих переменных на ограничениях, заданных как равенствами, так и неравенствами.

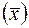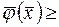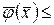Постановка задачи. Найти extr функции многих переменных f на замкнутом множестве 0

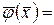0

0

Например, это замкнутое множество может иметь следующий частный вид:

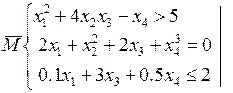здесь n-4, m-3

Задача 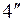является неклассической и называется задачей нелинейного программирования. В общем случае она решается только численным методом.

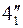Задача нелинейного программирования.

Постановка задачи. Найти extr квадратичной функции многих переменных 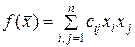(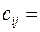const) на линейных ограничениях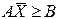

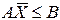, при .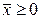

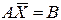
5. Нахождение extr функционала многих переменных на уравнениях связи без дополнительных ограничений на переменные.

Постановка задачи. Найти вектор 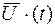, доставляющий extr функционалу

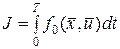на уравнениях связи

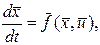t=0 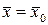: t=T,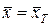

Если на переменные 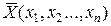и ограничений 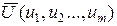нет дополнительных ограничений, то получается вариационная классическая задача оптимального управления, имеющая аналитическое решение.

6. Нахождение extr функции многих переменных на уравнениях связи сз дополнительными ограничениями на переменные.

Постановка задачи. Найти вектор 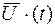, доставляющий extr функционалу 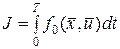на уравнениях связи

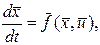t=0 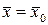: t=T,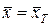

При дополнительных ограничениях на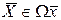

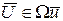
Это неклассическая вариационная задача оптимального управления и в общем случае не имеет аналитического решения.

Дата добавления: 2014-01-11