Примеры постановки задач управления

Пример 1. (Транспортная задача)

85% транспортных задач решаются линейным программированием

Из карьера К необходимо доставить на предприятие А, расположенного на станции железной дороги, исходное сырьё. Карьер стоит от железной дороги на расстоянии «φ». В какую точку М железной дороги выгоднее привести груз из точки станции чтобы потом его отправить по железной дороги, если стоимость перевозок на 1 км автотранспортом в «m» раз дороже чем по железной дороге (m>1 и R достаточно велико).

Рис. 8

Обозначим через X расстояние DM, получим , где СМ, путь который придется проделать грузу автотранспортом. Тогда по железной дороге останется проделать расстояние R-X (обращаем внимание на то обстоятельство, что мы рассматриваем только неотрицательные значения R-X, т.е. пункт назначения А левее М, очевидна, также нецелесообразно вести груз из с в точку , расположенную левее точки В).

Общая стоимость перевозок будет пропорциональна сумме

Нужно найти такое 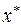из интервала [О, R ] изменения переменой х, которое минимизирует .

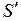Таким образом, данная транспортная задача математически представляет собой случай 2- нахождение «х» функций одной переменой С ограничениями (т.е. на замкнутом отрезке).

Пример 2. (Задача составления смеси).

Требуется составить смесь (например для производства картона либо удобрений и т.д.). Содержащею три вещества А, В, С. Известно что требуемая смесь должна содержать вещества А не менее 6 единиц, вещества В не менее 8 единиц, вещества с не менее 12 единиц. Вещества А, В, С имеются не в чистом виде, а содержатся в 3-х видах исходных продуктов –I, II, III –в концентрации указанной в следующей таблице.

	А[ед]	B[ед]	C[ед]
I x1
II x2
III x3	3.5	1.5

Вещество

Таблица 1

Стоимость единицы продуктов I, II, III различна: единица продукта I стоит 2 руб, продукта II – 3 руб и продукта III - 2,5 руб. Составить требуемую по составу смесь минимальной стоимости.

Обозначим число единиц продукта I входящего в смесь, через х₁, продукта II через х₂, продукта III – через х₃.

Составляемая смесь должна содержать вещество А, которое имеется во всех трех продуктах. На каждую единицу продукта I приходятся 2 части концентрации вещества. Следовательно если использовано х₁ единиц продукта I, то в составляемой смеси будет 2×1 частей вещества А. Наконец если использовано х₃ единиц продукта III, то в смеси будет 3,5 частей вещества А в смеси должно быть не менее единиц; то

2х₁+х₂+3,5х₃≥6.

Смесь должна содержать и вещество В, которое также содержится в этих трех продуктах. В каждой единице продукта I содержится 1 часть вещества В, следовательно, если используется х₁ единицы продукта I, то в смеси будет 1*х₁ частей вещества В. Соответственно, если использовано х₂ единицы продукта II, то в смеси окажется 2х₂ частей вещества В. Если же использовано х₃ единицы продукта III, то в смеси будет 1,5х₃ частей вещества В. С учетом того, что общее количество вещества В в смеси должна быть не менее 8 единиц, получаем

х₁+2х₂+1,5х₃≥8.

Рассуждая аналогично относительно концентрации вещества С, получаем, что 3 х₁+4х₂+2х₃≥12.

Стоимость смеси слагается из

2х₁ ру (стоимость использованного продукта I),

3х₂ руб (стоимость использованного продукта II),

2,5х₃ руб (стоимость использованного продукта III).

Следовательно общая стоимость смеси будет равна

F(x₁, x₂, x₃)=2х₁+3х₂+2,5х₃

Из физического смысла задачи следует, что число используемых продуктов всегда неотрицательно х₁≥0; х₂≥0; х₃≥0.

Итак, сведем все вместе.

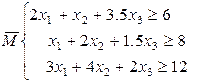
x_i≥0 (i=1, 2, 3)

F(x₁, x₂, x₃)=2х₁+3х₂+2,5х₃ →min

Найти х₁^*, х₂^*, х₃^*

Таким образом, математическая модель задачи, решают подсистему управления смесями, в данном конкретном случае представляют собой задачу 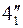,т.е. задачу линейного программирования.

Пример 3. Нажимное устройство реверсивного прокатного станка.

Схематично прокатка представляет собой пропуск слитка через вращающиеся валки, расстояние между которыми меньше толщины слитка. После окончания пропуска верхний волок перемещается в сторону нижнего и пропуск осуществляется заново. Процедура повторяется до тех пор, пока не получится лист заданной толщины. Нажимное устройство реверсивного прокатного станка осуществляется перемещением верхнего валка станка во время пауз между пропусками. Для каждой прокатываемой марки стали программа прокатки заранее известна. Поэтому режим работы приводного устройства характеризуется отработкой заданных следующих друг за другом перемещений при неизменной нагрузке, близкой к нагрузке холостого хода. Система управления нажимного устройства должна обеспечить максимальную производительность станка.

На рис. 10 представлена диаграмма,

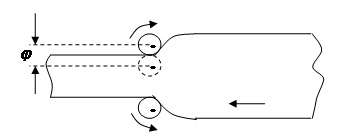
Рис. 9

характеризующая режим работы нажимного устройства. Заданное значение управляемой координаты – перемещение верхнего валка φ, отсчитываемые от его верхнего положения, представляемые собой ступенчатую функцию.

τ'_i – время на перестановку валка

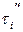– время собственной прокатки

Рис.10

Перед началом каждого пропуска в моменты времени t₁, t₂, …,t_n величина φ изменяется на требуемую перестановку валка. После последнего пропуска валок вращается в исходное положение для прокатки очередного слитка. Время τ_i, отведенное на каждый пропуск, можно представить состоящих из двух частей: первая часть 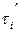отводится на перестановку верхнего валка, вторая часть 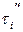- на собственную прокатку. Поскольку скорость вращения валков уже выбрана и осуществлена в прокатном стане, то сокращение времени нажимного устройства 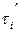позволяет сократить общее время прокатки слитка и, следовательно, увеличить производительность.

Время необходимое для отработки заданного перемещения, зависит от динамических свойств привода и от способа управления им. Поскольку привод уже выбран, то естественно поставить задачу об отыскании такого закона управления приводом, при котором время отработки будет минимальным.

Для привода нажимных устройств обычно применяются двигатель тока с независимым возбуждением, структурная схема которого приведена на рис.11

	Mнагр

Рис.11

См – коэффициент определяемый констр. Привода

Здесь i_я - ток якорь;

φ - перемещение нажимного устройства;

ω - угловая скорость этого перемещения S;

М_дв - движущий момент, М_дв = С_м· i_я

М_нагр - момент нагрузки;

J _p- момент инерции привода.

В правом приближении источник питания можно считать без инерционным. Можно пренебречь также индуктивностью цепи якоря двигателя. При принятых допущениях движения нажимного устройства описывается следующей системой дифференциального уравнения, которая соответствует структурной схеме рис.11

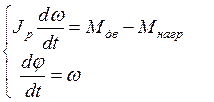
Пусть перемещение валка нажимного устройства должно изменяться от начального состояния t=0 φ=φ_i; ω=0 до заданного Необходимо так выбрать закон изменения управления воздействия -тока i_я, чтобы время перестановки было минимальным. Математически?.... управления можно выразить минимизацией формула

Тогда , где - время перестановки валка.

Данная конкретная перестановка задач лишена смысла до тех пор, пока не оговорены допустимые пределы изменения координат и воздействий системы т.е. якорного тока, скорости и перемещения может быть умешено до нуля. Однако в реальных условиях координаты воздействия ограничены.

Предельно допустимое значение тока, например, следует выбирать из следующих условий:

1) момент, развиваемый двигателем при выбранном максимальном значении тока, не должен превосходить пределов, определяемых механической погрешностью конструкции;

2) Значение тока не должно превосходить предельно допустимого по условиям коммутации;

3) Значение тока не должно выживать нагрева двигателя больше допустимого.

Из этих условий выбирают наиболее тяжелое, определяющее минимально допустимый ток I_m, и в процессе управления обеспечивают

.

Скорость привода ω также ограничена, поскольку у ограниченно напряжения источника питания. Кроме того, поскольку программа прокатки строго задана можно считать ограниченной и координату φ. Поэтому

Сведем все полученное выражение воедино

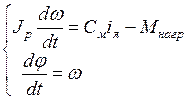, т.к. М_двиг=С_мi_я

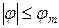
Найти , доставляющее минимум формулу J.

Видно, что задача о максимальной производительности прокатного станка сводится к 6-ой типовой задаче управления производством – неклассической вариационной задаче оптимального управления.

Вывод.

В данном разделе были рассмотрены типы производств, проанализированы задачи управления производством, осуществлена математическая постановка типовых задач управления. Выяснилось что первые четыре задачи (типовые) связаны с оптимизацией функций одной или многих переменных с ограничениями или без них и решение подобных задач рассматриваются в курсе «Методы оптимизации». Оставшиеся 2 задачи (типовые) связаны с оптимизацией ……. и называются задачами оптимальные управления.

Глава II. МЕТОДЫ РЕШЕНИЯ ЗАДАЧ УПРАВЛЕНИЯ

(ОТИМИЗАЦИЯ ФУНКЦИЙ Т.Е. ЗАДАЧИ 1-4)

Задача нахождения экстремума функций одной переменной

Дата добавления: 2014-01-11