Экстремум функции многих переменных на

открытом множестве М.

Задана некоторая функция многих переменных на открытом множестве М необходимо найти , принадлежащие открытому множеству М, и доставляющие экстремум функции . Эта задача нахождения безусловного экстремума функции многих переменных является аналогом задачи нахождения extr одной переменой на открытом интервале.

Так же как для задачи I дадим определение extr функции многих переменных.

Определение экстремума.

Функция , заданная на открытом множестве М, имеет в точке max(min), если эту точку можно окружить такой окрестностью , содержащиеся во множестве М, что для всех её точек , принадлежащих этой окрестности, выполняется неравенство:

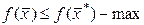
Как и задача I это определение extr не накладывает никак ограничений на класс функций . Для гладких же функций можно воспользоваться теоремой Ферма, которое дает следующие необходимое условие extr.

, , …, (*)

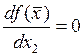В инженерной практике часто сложную нелинейную функцию аппроксимируют более простыми функциями, например, линейными или квадратичными.

Трудности решения задачи III существенно зависят от того, к какому классу функции относится исследуемая функция - к сепарабельным или несепарабельным.

Сепарабельными функциями называются такие функции 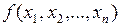, кторые могут быть записаны в виде:

,

Например,

В случае необходимые условия extr Ферма представляют из себя управления, каждое относительно одного неизвестного:

, , …,

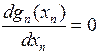
И таким образом, задача поиска n- мерного extr →к n задача поиска одномерного extr.

Для несепарабельных функций, т.е. функций с нелинейной связью переменной (например)

Уже должна работать теорема Ферма в общем виде (*).

Очень простым получается решение для сепарабельных квадратичных функций.

В этом случае решения

, где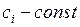

Пример.

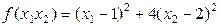
Найти и , доставляющие extr т.к. - сепарабильная квадратичная функция, то решение элементарно

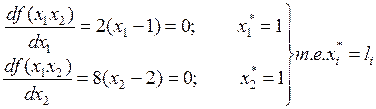
Отсюда ясна выгодность, если это представляется возможным, аппроксимация сложной поверхности сепарабильными квадратичными функциями.

Квадратичную функцию относительно «n» переменных можно представить как зависимость вида:

Ели обозначить 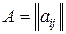- матрица коэффициентов: 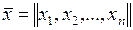- матрица строка, то выражение для квадратичной функции Z можно переписать в матричной форме

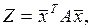где знак «Т» означает транспортирование матрицы-строки.

В настоящее время в задачах управления квадратичную функцию трактуют несколько шире, чем мы сделали это сейчас, и понимают под не комбинацию линейной и собственно квадратичной функции.

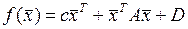, где

- матрица строка постоянных коэффициентов при ;

D- постоянный коэффициент.

Понятно, что это несепарабельная квадратичная функция. Её векторная производная по теореме Ферма должна быть равна нулю для экстремальных значений

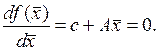
Это система линейных уравнений с равными коэффициентами. Решение её:

где

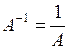
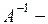матрица, обратная матрице H.

Это решение не всегда просто найти, особенно когда матрица H не является хорошо определенной (т.е. определитель этой матрицы или очень велик или очень мал). Кроме того, обращение матрицы, т.е. нахождение матрицы H, задача достаточно трудоемкая, в общем случае даже для ЭВМ.

Резюмируя, скажем, что хотя для несеперабельных квадратичных функций есть аналитическое решение, но нахождение в общем случае является достаточно трудоемкой задачей, поэтому зачастую трудоемкой задачей, поэтому зачастую прибегают к приближенным методам нахождения оптимальных значений таких функций.

Если же - неквадратичная несепарабельная функция многих переменных подразумевает, что решение существует и оно единственно. Установить существование и единственность решения можно на пути понятий выпуклости и вогнутости функций.

По аналогии с функций одной переменной для выпуклости функций многих переменных имеем

или уравнение касательной к поверхности

x₁

Это оценка функций снизу.

Для вогнутой функции имеем оценку сверху.

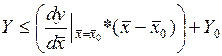
По аналогии же с функцией одной переменой имеет место следующая теорема:

Если функция -выпуклая, то на открытом множестве М она имеет единственный min, если же она вогнутая, то единственный max.

К сожалению, определение выпуклости или вогнутости функции многих переменных по приведенным выше оценка снизу или сверху неконструктивно, т.к. в общем случае при больших «n» определить знак неравенства бывает затруднительно.

1. Градиентные методы.

Различают градиентные методы I и II порядков. Мы начнем…

Градиент функции в некоторой точке- это вектор показывающий направление наибольшей скорости увеличения функции.

Антиградиент убывания функции (т.е. противоположно градиенту).

grad=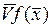, если спроектировать на ортогональные координаты оси.

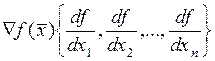
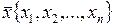
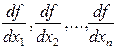-вектор строка

-антиградиент

-проекции grad

2.^* Возьмем 2-ую производную от (1-ая производная – градиент этой функции).

Гессиан

Это матрица Гессе или гессиан. По матрице Гессе можно судить о вогнутой или вогнутой функции по правилу Сильвестра или по собственным числам. **

Если все диагональные миноры положительные, то гессиан положительный определен (по критерию Cильвестра функция выпукла и имеет единственный min).

Если отрицательна, то все наоборот т.е. функция вогнута и единственный max.

Пример 1.

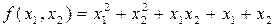
Это проекции градиента на оси.

Гессиан главные миноры

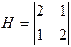
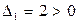
Следовательно, функция выпукла и имеет сильный min.

Теперь определим собственные числа

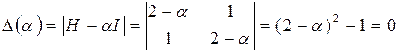
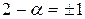
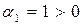
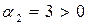
Собственные числа матрицы 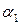и 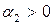, значит функция выпукла и имеет единственный (сильный) min

Пример 2.

имеет место слабый минимум

Пример 3

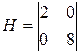
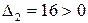
Выпуклый и единственный min.

Линии равного уровня функции многих переменных

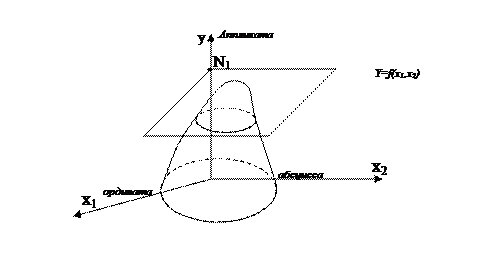
Предадим целевую функцию постоянного значения N₁, т.е это уравнение горизонтальной плоскости. Все аппликаты? Равны N₁. Множество точек для которых целевая имеет const значение называют линией равного уровня. Если возьмем ряд значений Y=N₁, N₂-N_n то получим семейство линий равного уровня. На будут интересовать проекции линий равного уровня

Приближенные методы нахождения безусловного extr функции многих переменных.

Этих методов очень много

1. Метод покоординатного спуска (подъема) – метод Зейделя- Гаусса (хорошо работает).

Пример.

Пусть , найти min по теореме Ферма.

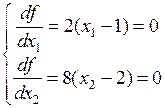
- точка безусловного экстремума

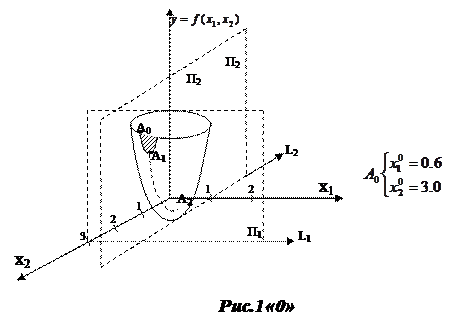
Метод поиск начинается с задания начальной точки. Математически начальную точку задают произвольно, а инженеры –начальное состояние системы.

Замораживаем на время шага одну из координат

1.

Плоскость П₁ расчет тело по параболе. Уравнение параболы найдем из целевой функции при

Нужно перейти из точки А₀ в А_{1 .} Найдем координату экстремума точки А₁.

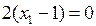
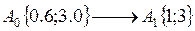
2.

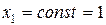
Плоскость П₂ проходит через А₁

Запишем уравнение параболы

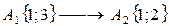
3.

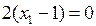
Пришли в точку экстремума и из неё не выходим.

Для сепарабельных функций поиск сходится за n –шагов, где n -число переменных.

Для сепарабельных квадрат функций оси параллельный осям координат.

Этот же метод рассмотрен для несепарабельных функций.

Пример. Рис «а»

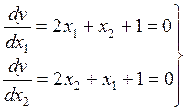
1)

Уравнение параболы

Экстремум частной параболы

2)

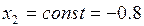
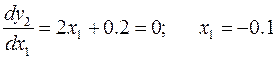
3)

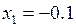
и т.д.

Для несеперабельных функций метод Гаусса-Зейделя сходится за бесконечное число шагов

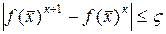
Это метод легко положить на алгоритм, но он имеет плохую скорость сходимости для несепарабельных функций, поэтому разработана группа градиентных методов. Различают градиентные методы 1-го и 2-го порядков.

Дата добавления: 2014-01-11