Свойства функционалов

Введем математическое понятие функционала. Будем говорить, что функционал задан, если указан закон, по которому каждой функции из некоторого класса функций поставлено в соответствие число. Например, для подынтегральной функции функционал есть некоторое число т.к.

то для другой подынтегральной функции функционал равен уже другому числу

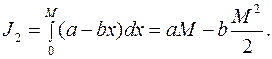
Таким образом, каждой подынтегральной функции соответствует свое значение функционала. Если нарисовать график функционала, то мы должны отметить, что аргументом функционала является функция 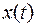и, следовательно, каждая точка на оси абсцисс на отрезке представляет собой некоторую функцию из определению класса функции, и каждому значению аргумента т.е. функции соответствует значению функционала из отрезка 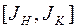т.е. число.

Рис.5

Для функций, являющихся аргументами функционала, введем определения.

Множество всех функций, обладающих определенными свойствами, называются функциональным пространством. Мы будем использовать следующие функциональные пространства.

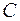- представляет множество непрерывных функций 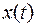ч определенных на отрезке ;

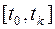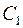- состоит из непрерывных функций 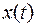определенных на отрезке 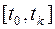и имеющих на этом отрезке непрерывную 1-ую производную;

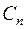– состоит из функций, непрерывных на отрезке 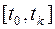и имеющих на этом отрезке непрерывные производные до порядка «n» включительно.

Каждое из пространств специальным образом нормируется т.е. каждой функции 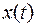, входящей в пространство, ставится в соответствующие некоторое неотрицательное число , называемое нормой.

В каждом пространстве норма определяется по своим правилам:

для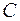

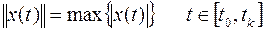
для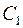

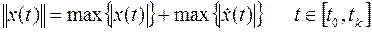
для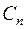

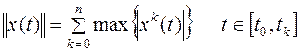
Введенные нормы функции обладают следующими свойствами:

1) , причем 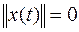только для

2) , где 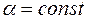- некоторое число

3) 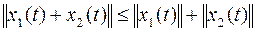- неравенство треугольника

С помощью норм можно определить «расстояние» между функциями внутри функционального пространства:

Функционал называется непрерывным в «точке» (т.е. для функции) , если для любого сколько угодно малого числа 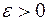можно указать такое число 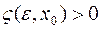, что при 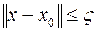будет справедливо .

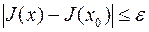Норма - максимальное «различие» между и . Геометрический смысл непрерывности- при малых изменениях функции 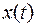изменения площади должны быть тоже малы (т.е. площадь не должна изменяться скачком). Функционал называется непрерывным в области если он непрерывен в каждой «точке» (а точка представляет собой функцию) этой области.

Функционал называется линейным, если выполняются следующие два условия:

а) аддитивности, т.е. для любых функций и из области определения функционала справедливо

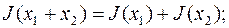
б) однородности, т.е. для любого числа 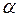справедливо

Примеры.

1. Функционал 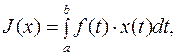где

- произвольная непрерывная функция, является непрерывным и линейным в пространстве , т.е. в пространстве непрерывных функций 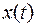, заданных на отрезке . Легко видеть, что свойства линейности функционала аддитивности и однородность – выполняются для рассматриваемого случая.

2. Функционал где и - непрерывные на отрезке функции, являются линейными в пространстве , т.е. в пространстве непрерывных дифференцируемых функций 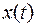, заданных на отрезке.

3. Функционал 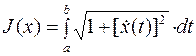-будет непрерывным нелинейным функционалом в пространстве

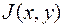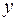Рассмотрим билинейные и квадратичные формулы. Функционалом 2-х переменных называются билинейными, если он являются линейным от при фиксированном и линейной 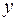при фиксированном .

Таким образом, для билинейного функционала 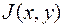имеют место равенства, отражающие свойства аддитивности и однородности:

.

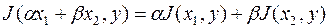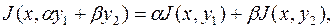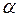где и 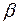- произвольные числа. Билинейный функционал, в котором 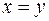, называется квадратичным.

Пример.

4. 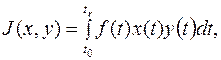где функции 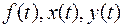- принадлежат пространству 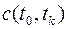. Для функционала выполняются свойства аддитивности и однородности

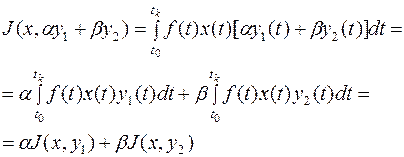
Аналогично можно доказать, что 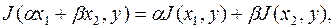т.е. рассматриваемый функционал билинейный, а соответствующий ему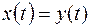

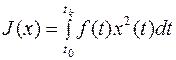- квадратичный.

Свойство функционалов характеризуется следующими леммами, которые мы рассмотрим без доказательства.

Лемма 1 (лемма Лагранжа).

Пусть -некоторая непрерывная на отрезке функция. Если линейный функционал

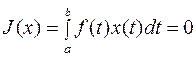для любой 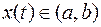такой, что то .

Лемма 2

Если квадратичный функционал

для любой функции , имеющей кусочно-непрерывную производную и удовлетворяющей условию 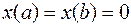, то функция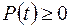 для любого 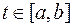. Здесь 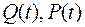- непрерывные функции на отрезке .

Введем понятия дифференцируемости и дифференциала функционала.

Функционал , определенный в линейном нормированном пространстве , называется дифференцируемым в «точке» (т.е. функции) , если существует такой линейный относительно приращений 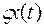функционал 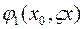, что для любого допустимого приращения

функции приращение функционала имеет вид

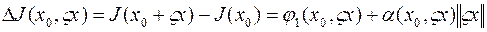
причем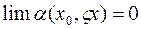

Линейный относительно приращения 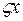функционала 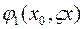называется дифференциалом функционала или его 1-ой вариацией и обозначается

. Итак, еще раз.

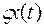Аргументу функционала дается приращение . Приращение функционала разлагается в ряд Тейлора. Линейна часть разложения 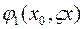, называется дифференциалом или 1-ой вариацией функционала.

Функционал является дифференцируемым в некоторой области функционального пространства , если он дифференцируем в каждой точки этой области. Отметим, что в функциональном анализе линейный функционал 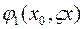носит название сильного дифференциала (дифференциала Фреше) в отличие от слабого дифференциала (дифференциала Гато).

Функционал называется дважды дифференцируемым в точке , если для любого допустимого приращения аргумента приращение функционала можно представить в виде

где 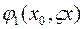- линейный функционал относительно приращений - квадратичный функционал относительно приращения 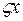, кроме того

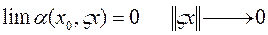
Квадратичный функционал называется вторым дифференциалом функционала в точке или второй вариацией и обозначается

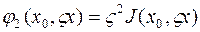
Функционал будет дважды дифференцируемым в области , если он дважды дифференцируем в каждой точке этой области. Первая и вторая вариации функционала, если они существуют, определяются единственным образом.

Дата добавления: 2014-01-11