Точка на прямой

Классификация прямых

Прямая

Лекция № 2. ПРЯМАЯ И ПЛОСКОСТЬ

Система знаков

Система прямоугольных (декартовых) координат

Точка определена в пространстве тремя координатами:

Х - расстояние от точки А до плоскости П₃ (абсцисса точки – АА₃),

Y - расстояние от точки А до плоскости П₂ (ордината точки – АА₂),

Z - расстояние от точки А до плоскости П₁ (аппликата точки – АА₁).

 

Октант	Х	Y	Z
	+	+	+
	+	-	+
	+	-	-
	+	+	-
	-	+	+
	-	-	+
	-	-	-
	-	+	-

  Пример. Используя правило знаков, определить, в какой четверти находятся точки А, В и С. А (+ + +) –? октант, В (+ - -) –? октант, С (+ - +) –? октант.  

План лекции

1. Прямая.

1.1. Проекции прямой.

1.2. Классификация прямых.

1.3. Точка на прямой.

1.4. Деление отрезка в данном отношении.

1.5. Следы прямой.

2. Проекции плоскости.

2.1. Способы задания плоскости.

2.2. Следы плоскости.

2.3. Классификация плоскостей.

2.4. Линии в плоскости.

2.5. Главные линии плоскости.

1.1. Проекции прямой

Прямая в пространстве безгранична. Ее положение определяется двумя точками. На чертеже прямую определяют двумя проекциями прямой: l (A₂B₂; А₁В₁) (рис. 2.1). Проекции прямой проходят через одноименные проекции точек, которыми она задана. Проекциями прямой могут быть прямая или точка. В последнем случае прямая расположена перпендикулярно к плоскости проекций.

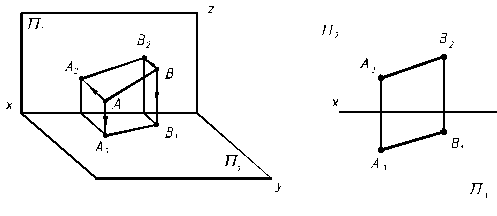
Рис. 2.1

Прямую на эпюре можно задавать не только проекциями ее отрезка, но и проекциями некоторой произвольной части прямой. При этом проекцию обозначают одной буквой l (l₁, l₂), (рис. 2.2)

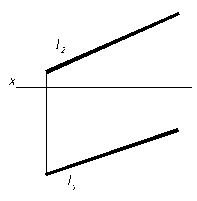
Рис. 2.2

По своему положению относительно плоскостей проекций прямые подразделяются на:

прямые общего положениячастного положения

прямые не | | и не ^ уровня проецирующие

ни к одной из плоскостей

проекций

Прямые общего положения проецируются на плоскости проекций с искажением, причем проекции отрезка всегда меньше самого отрезка (рис. 2.1, рис. 2.2).

Прямые уровня – это прямые | | одной из плоскостей проекций. Они подразделяются на

прямые:

1. Горизонтального 2. Фронтального 3. Профильного

уровня уровня уровня

АВ | | П₁ АВ | | П₂ АВ | | П₃

(рис. 2.3) (рис. 2.4)

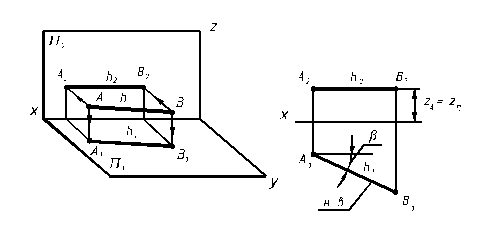Рис. 2.3

ZA=ZB, Ù A2B2 | | x, β = AB П2

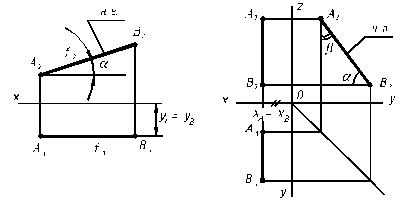
yA= yB Ù A1B1| | x a = AB П1

xA= xB A2B2 | | z, A1B1 | | y

Рис. 2.4

Прямые Î одной из плоскостей проекций называются прямыми нулевого уровня.

АВÎ П₁ CDÎ П₂

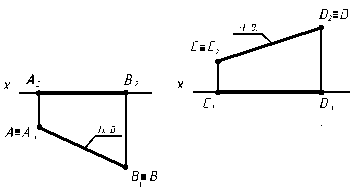
Рис. 2.5

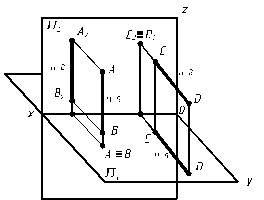
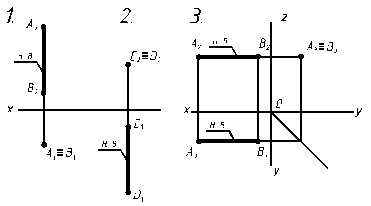
Проецирующие прямые – это прямые ^ к одной из плоскостей проекций (и | | двум другим плоскостям проекций).

Проецирующие прямые

1. Горизонтально- 2. Фронтально- 3. Профильно-

проецирующие проецирующие проецирующие

АВ ^ П₁ CD ^ П₂ АВ ^ П₃

A₂B₂ ^ x C₁ D ₁ ^ x A₁B₁ ^ y, A₂B₂ ^ z

α = 90⁰ β = 90⁰ γ = 90⁰

β = 0 α = 0 α = 0, β = 0

Рис. 2.6

Аксиома (принадлежности). Если точка принадлежит прямой, то одноименные проекции точки принадлежат одноименным проекциям прямой.

Пример. Определить, какие из заданных точек Î прямой L.

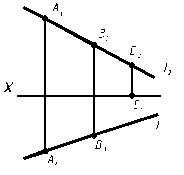
B Î l, т. к. B1Î l1, B2 Î l2

Рис. 2.7

1.4. Деление отрезка в данном отношении

Теорема. Если точка делит отрезок прямой в данном отношении, то проекции этой точки делят проекции данной прямой в том же отношении.

Пример. Разделить отрезок АВ точкой С в отношении 2:3, считая от точки А.

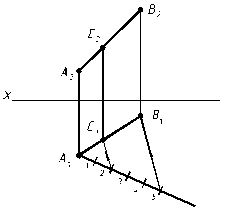
АС: СВ=2:3

Рис. 2.8

Из горизонтальной проекции точки А проводим вспомогательную прямую и откладываем на ней 5(2+3) отрезков произвольной длины, но равных между собой.

Проводим отрезок 5В₁ и | | ему через точку 2 проводим прямую до пересечения с горизонтальной проекцией прямой А₁В₁. Получаем проекцию точки С₁ и затем точку С₂ , таким образом, точка С делит отрезок АВ в отношении 2:3.

Для профильных прямых необходима проверка по третьей проекции.

1.5. Следы прямой

Следом прямой называется точка пересечения прямой с плоскостью проекций.

Прямая общего положения в системе трех плоскостей проекций имеет три следа: горизонтальный, фронтальный и профильный.

Прямая не имеет следа на плоскости проекций, если она | | этой плоскости проекций.

Для построения горизонтального следа прямой необходимо продолжить прямую до пересечения с горизонтальной плоскостью проекций П₁ , при этом горизонтальная проекция горизонтального следа М₁ совпадает с самим следом М, а фронтальная проекция горизонтального следа М₂ лежит на оси проекций х. Аналогично, для построения фронтального следа N необходимо продолжить прямую до пересечения с фронтальной плоскостью проекций, при этом фронтальная проекция N₂ фронтального следа N совпадает с самим следом, а горизонтальная проекция фронтального следа N₁ лежит на оси проекций.

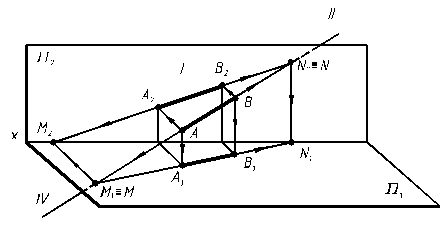
Рис. 2.9

Правило. Чтобы построить горизонтальный след прямой М, необходимо фронтальную проекцию прямой продолжить до пересечения с осью х и получить фронтальную проекцию горизонтального следа М₂. Из полученной точки восстановить или опустить ^ до пересечения с продолжением горизонтальной проекции прямой. Получаем горизонтальный след М, совпадающий с ее горизонтальной проекцией М₁.

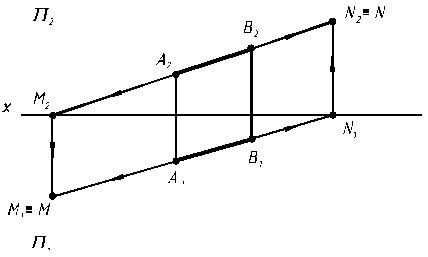
Рис. 2.10

Дата добавления: 2014-01-11