Примеры систем автоматического управления. Рассмотрим некоторые наиболее простые примеры объектов управления

Рассмотрим некоторые наиболее простые примеры объектов управления.

Гидравлический резервуар, пример простейшего объекта автоматического управления, показан на рисунке 1.2.1, а. Управляющим воздействием x является скорость притока воды в резервуар Q; управляемой величиной y — уровень воды в ре­зервуаре H, а внешним возмущением — расход воды из резер­вуара G.

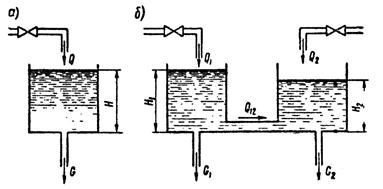
Рисунок 1.2.1 – Схема гидравлического резервуара

Между величинами Q, H и G может быть написана следующая зависимость:

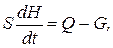(1.2.1)

где S — площадь поперечного сечения резервуара.

Уравнение (1.2.1) представляет собой математическое описание рассматриваемого простейшего объекта. Легко заметить, что рассматриваемый объект нейтрален, так как пр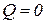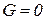и , и 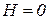, кратковременное увеличение Q (после сни­жения Q до нуля) приведет к повышению уровня H и пере­ходу к новому состоянию 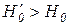, что соответствует гра­фику, показанному на рисунке 1.1.3, в. Так как возрастание Q приводит к увеличению 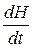, то характеристика объекта яв­ляется монотонной.

При наличии двух сообщающихся резервуаров (рисунок 1.2.1, б) объект будет описан системой уравнений:

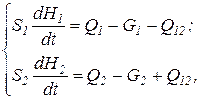(1.2.2)

где 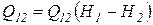представляет собой некоторую в об­щем случае нелинейную монотонную функцию.

Уравнения (1.2.2) представляют собой математическое опи­сание объекта, в котором каждый из векторов управляемых величин и воздействий имеет по две компоненты

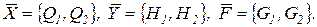
При этом каждый из уровне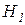й и 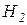зависит от величин 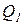, , 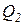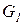и 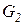и, следовательно, объект многосвязный.

Печи (топливные и электрические). Более сложным объектом управления является печь, нагрев которой производится путем сжигания топлива (рисунок 1.2.2).

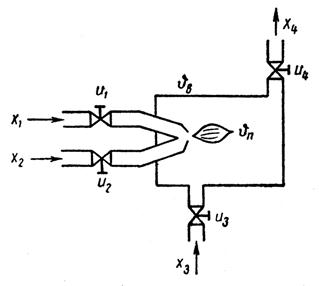
Рисунок 1.2.2 – Схема печи

Для печи регулируемой величиной является температура в определенных точках 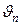. Управляющими величинами служат положения вентилей и шиберов 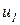, , 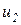, , 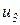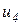регулирующих подачу горючего, приток воздуха и вытяжку газов. Внешними воздействиями являются изменения в составе и расходе горючего, в давлении воздуха системы, изменения тепловых параметров, связанных с загрузкой и выгрузкой печи. Некоторые из этих величин могут контролироваться (например, расходы и темпе­ратура), однако большинство не поддается контролю.

Тепловой режим печи описывается сложной систе­мой дифференциальных уравнений в частных произ­водных, которые обычно дают приближенное представление о характере про­цессов в печи.

В приближенных расчётах систем, в которых уп­равление ведется только путем изменения скорости подачи горючего в пламен­ных печах или мощности электрических нагревателей в электрических печах, математическое описание объекта может быть сведено к дифференциальному уравнению первого порядка.

Если управляющая величина Q — количество тепла, выделяемого в печи за единицу времени, а 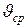— средняя температура печи (рисунок 1.2.3, а), то уравнение теплового баланса может быть при­ближенно записано как

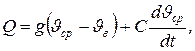(1.2.3)

где C — объемная теплоёмкость печи, g — коэффициент теплопроводности системы печь – окружающая среда, температура которой .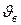

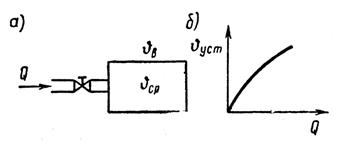
Рисунок 1.2.3 – Печь как объект управления (а) и статическая
характеристика печи (б)

Распределенный характер системы печь – нагреваемая де­таль приближённо учитывается введением некоторого запазды­вания между средней температурой печи 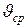и температурой детали или некоторой точки печи 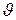, являющейся регулируемой величиной, измеряемой в процессе управления

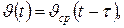(1.2.4)

где τ — некоторое эквивалентное время запаздывания.

В общем случае параметры печи g и C зависят от темпера­туры и только в приближенных расчётах могут быть приняты постоянными.

Неконтролируемыми воздействиями являются изменения окружающей внешней температуры 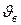, изменения теплоёмкости печи C и изменения условий теплообмена g.

Зависимость между установившейся температурой печи 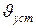и количеством тепла, выделяемого в печи за еди­ницу времени Q, выра­жается монотонной стати­ческой характеристикой управления (рисунок 1.2.3, б).

Несколько сложнее опи­сать математически процесс в электрических печах ра­диационного нагрева по­верхности различных изде­лий. На рисунке 1.2.4 схемати­чески показана система радиационных нагревате­лей, излучающих тепло для нагрева поверхности мас­сивного тела. Мощность, излучаемая на единицу по­верхности изделия, в тепло­вых единицах

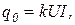
где U и I — соответственно напряжение и ток нагревателей; k — коэффициент пропорциональности, зависящий от излучателя и обратно пропорциональный поверх­ности облучения.

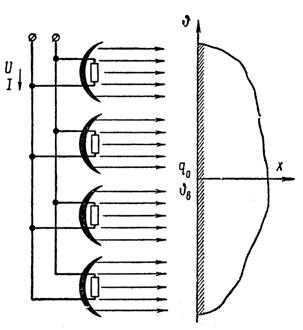
Рисунок 1.2.4 – Схема системы радиационных нагревателей

Управляющим воздействием служит напряжение питания излучателя U. Удельная мощность

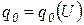
нелинейно зависит от напряжения питания.

Управляемой величиной является температура нагрева по­верхности изделия.

Внешние, большей частью неконтролируемые воздействия — различие в параметрах нагреваемых изделий, изменения параметров излучателей, условий теплоотвода с поверхности изде­лия и т.п.

Тепловой режим нагрева поверхности материала приближённо описывается одномерным уравнением Фурье для полуограниченного тела

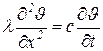(1.2.5)

при начальных условиях

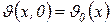(1.2.6)

и граничных условиях, определяемых теплообменом на поверхности изделия,

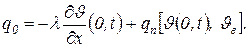(1.2.7)

В уравнениях (1.2.5–1.2.7) приняты следующие обозначе­ния: c и λ — соответственно удельная объемная теплоемкость и удельная теплопроводность нагреваемого материала; x — коор­дината точки материала, отсчитываемая от его поверхности; 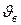— температура воздуха, омывающего поверхность материала; 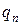— плотность теплового потока отвода тепла от поверхности тела в окружающее пространство, зависящая от температуры поверхности 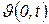и окружающей температуры .

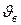Решение этих уравнений дает возможность ориентировочно судить о переходных процессах нагрева деталей.

Рассмотренные примеры печей относятся к категории устой­чивых объектов с самовыравниванием.

Дата добавления: 2014-01-11