Свойства функции распределения

Пусть F (x) – функция распределения случайной величины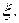

1) ;

2) ;

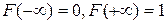3) F (x) – неубывающая функция;

4) F (x) непрерывна слева;

5) .

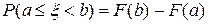Доказательство. Неравенства 1 следуют из того, что F (x) – вероятность. Событие , а 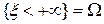, следовательно, свойства 2 следуют из равенств 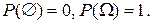Если x < t, то . Следовательно, из свойства вероятности следует, что 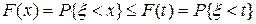. Доказательство 4 опускаем. Докажем свойство 5. +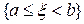=и события и 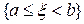несовместны, значит 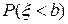=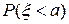+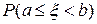. Откуда следует .

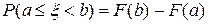3.2 Дискретные случайные величины

Случайные величины в дальнейшем будем обозначать большими латинскими буквами: X, Y, Z, ….

Случайная величина называется дискретной, если в результате испытания она может принять значение из конечного либо счетного множества возможных числовых значений. Будем пользоваться сокращением ДСВ для обозначения дискретной случайной величины.

Закон распределения ДСВ Х можно задать в виде функции, ставящей в соответствие каждому значению x_i ее вероятность p_i = P (X = x_i), причем .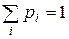

Когда различных значений ДСВ конечно и равно n, то ее закон распределения задается в виде таблицы ():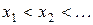

x 1	x 2	…	x n
p 1	p 2	…	p n

Очевидно, должно выполняться равенство .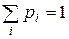

Построим функцию распределения для ДВС. По определению

.

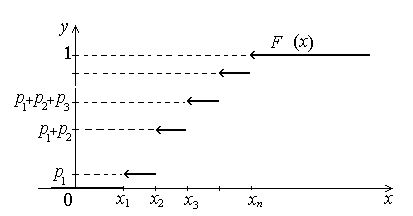График функции распределения ДВС Рисунок 3.1  

т.е. для любого действительного х значение F (x) численно равно вероятности наступления следующего события: в результате испытаний над X она приняла значение строго меньшее x. Эта функция является кусочно-постоянной (ступенчатой), ее график см. на рисунке 3.1.

Пример 3.1 Х – число очков, выпавшее при однократном вбрасывании игрального кубика. Закон распределения Х имеет вид

		…
		…

Это так называемое равномерное дискретное распределение.

Пример 3.2 Х – число успехов в схеме Бернулли. Пусть n – число испытаний, p – вероятность успеха, q =1– p. Тогда закон распределения случайной величины Х задается соответствием , i =1, …, n. Студенту предлагается доказать, что . Этот закон называется биномиальным и будем в дальнейшем обозначать B(n, p).

Пример 3.3 Х – число обращений клиентов в сервисный центр по ремонту бытовой техники фирмы SONY (см. пример 1.2). Из практики следует, что закон распределения имеет вид , i = 0, 1, …. Это распределение называется распределением Пуассона и будем в дальнейшем обозначать P (l). Студенту предлагается доказать, что .

3.4 Непрерывные случайные величины

Будем рассматривать пространство элементарных событий как совокупность всех точек числовой оси. Случайная величина X называется непрерывно распределенной (или непрерывной), если ее функция распределения является непрерывной. Для непрерывной случайной величины примем сокращение НСВ.

Примеры. X – время безотказной работы телевизора (см. пример 1.3). X – рост взрослого человека.

Пусть X – НСВ. Найдем вероятность того, что в результате испытаний случайная величина X примет значение a Î R. Докажем, что P (X = a)=0.

Так как 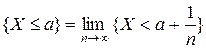, то .

Следовательно

=.

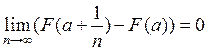Заметим, что в случае ДСВ вероятность P (X = a) не всегда равна нулю.

Дата добавления: 2014-01-11