Плотность распределения вероятности НВС

Ранее говорилось, что функция распределения задает закон распределения случайной величины. Для НСВ удобнее закон распределения задавать при помощи плотности распределения вероятности. Плотностью распределения вероятности НСВ Х называется предел (если он существует)

.

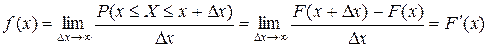Таким образом, плотность распределения является первообразной для функции распределения.

Свойства плотности вероятности.

1. Плотность вероятности является неотрицательной функцией.

Действительно, производная неубывающей функции неотрицательна.

2. 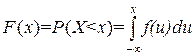. Это следует из того, что плотность распределения является первообразной для функции распределения.

3. 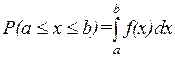. Это следует из формулы Ньютона-Лейбница:

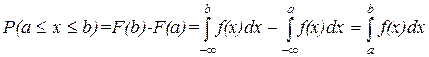
4. 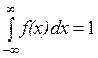. Это свойство называется свойством нормировки.

Действительно,.

Пример 3.4 Случайная величина Х называется равномерно распределенной на отрезке [a, b], если ее плотность распределения имеет вид

В дальнейшем равномерное распределение будем обозначать R(a, b).

Рисунок 3.2  

График плотности и функции распределения приведены на следующих рисунке 3.2.

Пример 3.5 Экспоненциальное (или показательное) распределение имеет плотность распределения вида

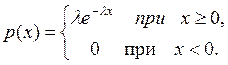
В дальнейшем показательное распределение будем обозначать E(l).

Из практики известно, что время безотказной работы телевизора распределено по показательному закону. Смысл параметра l в том, что число 1/ l равно среднему времени безотказной работы телевизора.

.

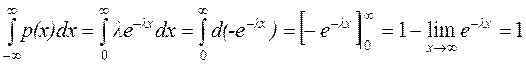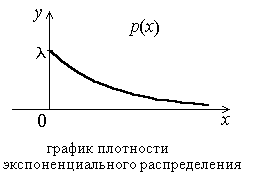Рисунок 3.3

3.3 Числовые характеристики случайных величин

Числовые характеристики ДСВ. Пусть дана ДСВ X своим законом распределения x_i ® p_i. Математическим ожиданием ДВС X называется число 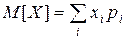. М.о. – сокращение словосочетания “математическое ожидание”.

Смысл математического ожидания заключается в следующем: это вероятностное среднее значение случайной величины.

Дисперсией ДСВ X называется математическое ожидание квадрата отклонения ДСВ от ее математического ожидания:

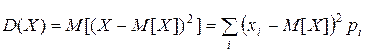
Смысл дисперсии в том, что она является мерой рассеяния значений случайной величины от математического ожидания. Чем меньше дисперсия, тем меньше разброс значений от математического ожидания.

Сренеквадратическим отклонением случайной величины Х называется число 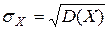. С.к.о. – сокращение словосочетания “Сренеквадратическое отклонение”.

Эта величина более точно характеризует степень рассеяния значений случайной величины от математического ожидания, чем дисперсия. Обоснуйте почему?

Числовые характеристики непрерывных случайных величин. Пусть имеется НСВ X с плотностью распределения f (x).

Математическим ожиданием НСВ X называется число .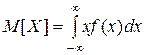

Дисперсией НСВ X называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

.

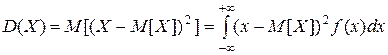Сренеквадратическим отклонением случайной величины Х называется число .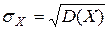

Смыслы м.о., дисперсии, с.к.о. для НСВ те же, что и для ДСВ.

Лекция 4

4.1 Действия над случайными величинами

1. Сумма (разность) случайных величин. Пусть Х, Y – случайные величины с функциями распределения F_x (x) и F_y (y) соответственно. Суммой Z = X ± Y называется с.в. Z с функцией распределения F_z (z)= P(X ± Y<z).

2. Произведением с.л. Х, Y называется с.в. Z = X Y с функцией распределения F _z(z)= P (XY < z).

3. Произведением числа С на с.в. Х называется с.в. Z = СХ с функцией распределения F _z(z) = P (СХ < z).

4.2 Независимые случайные величины. Пусть Х, Y – случайные величины с функциями распределения F_x (x) и F_y (y) соответственно. Функцией совместного распределения двух с.в. Х, Y называется функция от двух переменных

.

Здесь под { X < x, Y < y } понимается произведение событий { X < x } и { Y < y }.

Плотностью совместного распределения непрерывных с.в. Х, Y называется функция

.

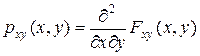С.в Х, Y называются независимыми, если

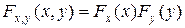. (4.1)

Из этого равенства следует, что . По определению условной вероятности

.

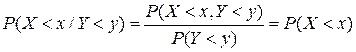Смысл этого равенства состоит в том, что независимость с.в. Х, Y означает, что закон распределения одной из них не изменяется от того, какое значение приняла другая в результате проведения опыта.

Если с.в. Х, Y – НСВ с плотностями 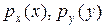соответственно, то их независимость означает

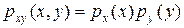
(4.2)

Для ДСВ Х, Y их независимость означает

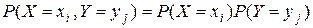
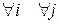(4.3)

4.3 Свойства математического ожидания

Доказательства свойств проведем для ДСВ.

1. M [ C ]= C, где С =const. Действительно, P (X = C)=1. M [ C ]= C P (X = C)= C.

2. M [ CX ]= C × M [ X ], С – константа.

Закон распределения с.в. СХ имеет вид: С x_i ® р_i. Тогда

.

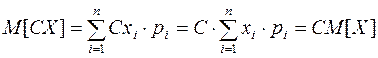3. M [ X + Y ]= M [ X ]+ M [ Y ]. В частности, M [ X + a ]= M [ X ]+ a, a =const.

Обозначим 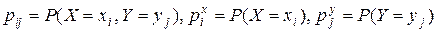. Тогда

=

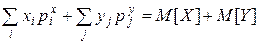
В предпоследнем равенстве воспользовались свойством .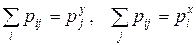

4. M[X]×M[Y] = M[X]×M[Y], если с.в. X,Y независимы.

Поскольку X, Y независимы, то из (4.3) следует 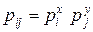. Тогда

.

5. Пусть с.в. Y является функцией j (X) от с.в. X. Тогда для верны формулы

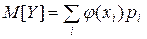для ДСВ,

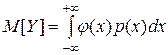для НСВ.

Действительно, закон распределения с.в. Y имеет вид 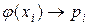. Все равные значения 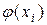заменяются одним, а соответствующие вероятности складываются. Тогда по определению м.о. .

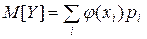Пример. 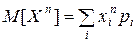для ДСВ и 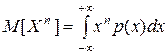для НСВ.

Дата добавления: 2014-01-11