Другие числовые характеристики

Свойства дисперсии

1. .

2. .

3 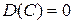, C =const.

4. 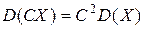, C=const.

5. D (X+Y) =D (X)+ D (Y), если с.в. X,Y независимы.

В частности, D (X+C) =D (X), C =const;

Докажем равенство 1.

=.

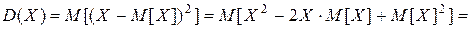
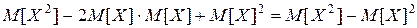Использованы свойства м.о. и тот факт, что M [ X ] = const.

Доказательство 5. По свойству 1 имеем D (X+Y) =M [(X + Y)²]– (M [ X ]+ M [ Y ])²=

=

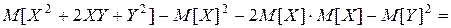
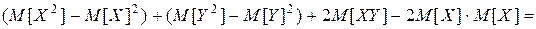
По свойству 4 м.о. .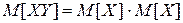

=.

Начальным моментом k-го порядка случайной величины X называется математическое ожидание случайной величины X^k

.

Заметим n₁= M [ X ].

Центральным моментом k-го порядка называется .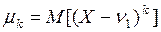

Заметим, что .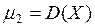

Медиана – это такое число Ме (Х), что F (Ме (Х)) = 0,5.

Мода – точка максимума плотности распределения. Если у с.в. одна мода, то распределение называется унимодальным.

Квантилью порядка a (0<a<1) называется такое число x _a, что F (x _a) = a. Заметим, что квантиль порядка 0,5 совпадает с медианой.

Коэффициентом асимметрии называется число .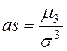

Коэффициентом эксцесса называется число .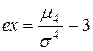

4.6 Нормальное распределение (распределение Гаусса)

Случайная величина Х называется нормально распределенной (имеющей распределение Гаусса), если ее плотность вероятности имеет вид

.

Нормальное распределение будем обозначать N(a, s). Тогда X ÎN(a, s) означает, что с.в. X имеет нормальное распределение с параметрами a, s. Плотность зависит от двух параметров a и s > 0, смысл которых выясним в дальнейшем.

Функция распределения равна

.

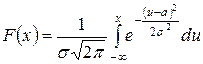Докажем, что плотность распределения удовлетворяет свойству 4 нормировки плотности распределения (лекция 3).

График плотности нормального распределения см. на рисунке 4.1.

Рисунок 4.1  

Если параметры a = 0, σ = 1, то такая нормально распределенная случайная величина называется стандартной нормальной случайной величиной.

В природе часто встречаются нормально распределенные с.в. Так, «естест-венные» размеры человека (рост, вес и т.д.), деревьев (высота, диаметр ствола) распределены нормально. Причина этого явления раскрывается в теореме Ляпунова, о которой речь пойдет в дальнейшем.

Лекция 5

5.1 Числовые характеристики некоторых распределений

Биномиальное распределение. Это распределение рассматривалось в примере 3.2 (лекция 3). Пусть Х – распределена по биномиальному закону с параметрами n, p (n – число испытаний, p –вероятность успеха), q =1– p. Рассмотрим с.в. Х_i c законом распределения 0® q, 1® p (i = 1,2, …, n). Математическое ожидание 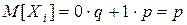. Случайная величина , причем с.в. независимы и распределены одинаково. Следовательно,

.

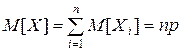Вычислим дисперсию .

.

Итак,

.

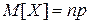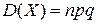
Распределение Пуассона. Пуассоновский закон распределение имеет вид , x_i = i = 0, 1, ….

.

==

=.

Итак,

. .

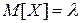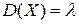Равномерное распределение.

.

.

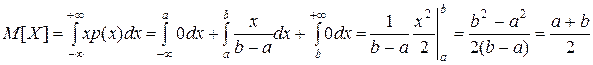Итак,

. .

Показательное распределение.

=.

.

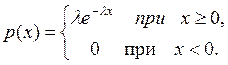
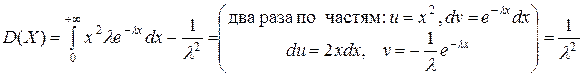Итак,

. .

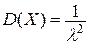Нормальное распределение.

.

Аналогично можно вычислить дисперсию .

Итак,

. .

5.2 Вероятность попадания с.в. в числовой промежуток

Пусть Х – ДСВ. Тогда .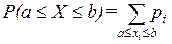

Рассмотрим НСВ Х. Так как для любого числа с, то для НСВ вероятности ===.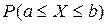

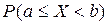Для вычисления вероятности 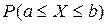можно применить две формулы:

,

.

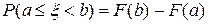Если интеграл “берущийся”, то никаких проблем не возникает. Для нормального распределения вопрос вычисления вероятности 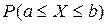стоит особо, так как интеграл получается не “берущийся” и на практике часто приходится вычислять эту вероятность.

Предварительно рассмотрим функцию Лапласа, вычислению которой приводится задача вычисления вероятности для нормального распределения.

Функцией Лапласа называется функция

.

Дата добавления: 2014-01-11