Метод замены плоскостей проекций. Сущность метода замены плоскостей проекций заключается в том, что одна из плоскостей проекций системы П!/П2 (или последовательно обе) заменяется новой

Сущность метода замены плоскостей проекций заключается в том, что одна из плоскостей проекций системы П_!/П₂ (или последовательно обе) заменяется новой плоскостью, перпендикулярной к плоскости оставшейся. Положение заданных геометрических элементов в пространстве при этом не изменяется. Образуется новая система плоскостей проекций П₁/П₄ (П₂/П₅).

На рисунке 75 показано проецирование точки на плоскости П₄ и П₅. Плоскость П₄ перпендикулярна плоскости П₁.

[АА₁]=[А₂А_х]=[А₄А_х1],т.е.

расстояние от новой фронтальной проекции до новой оси равно расстоянию от старой фронтальной проекции точки до старой оси.

Рисунок 75 Рисунок 76

При построении эпюра в новой системе, новая проекция точки А₄ и старая проекция точки А₁ (или А₅ и А₂) расположены на одном перпендикуляре к новой оси.

Пример 1. Определить длину отрезка АВ и угол наклона его к плоскости П₁ и П_2.

Решение задачи показано на рисунке 76.

Введена плоскость П₄ перпендикулярно П₁ и параллельно отрезку АВ, т. к. Х₁ параллелен А₁В₁. А₁А₄ и В₁В₄ находятся на одной линии связи перпендикулярной новой оси Х₁. Отрезки А₂А_х=А₄А_х1; В₂В_х=В₄В_х1. Отрезок[А₄В₄] =[АВ] –длина отрезка.

Углы наклона показаны на чертеже. a - угол наклона к П_1; b- угол наклона к П_2.

Для решения некоторых задач требуется вводить поочередно замены двух плоскостей проекций.

Пример 2. Определить истинную величину треугольника АВС.

Последовательность решения задачи на рисунке 77.

Рисунок 77

1) Введена плоскость П_{4 ┴} П₁; П₂ /П₁ П₄/П₁

Плоскость П₄ перпендикулярна плоскости треугольника АВС, так, как она перпендикулярна горизонтали, проведенной в треугольнике. На плоскости П₄ проекция треугольника А₄В₄С₄- прямая линия, угол - угол наклона плоскости АВС к горизонтальной плоскости проекций П₁.

[А₂А_х]=[А₄А_х1]; [В₂В_х]=[В₄В_х1]; [С₂С_х]=[С₄С_х1].

2) Введена плоскость П_{5 ┴} П₄. П₄/П₁ П₅/П₄

Плоскость треугольника АВС стала параллельна плоскости П₅ т.к. Х₂ параллельна А₄В₄С₄.

[А₁А_х1]=[А₅А_х2]; [В₁В_х1]=[В₅В_х2]; [С₁С_х1]=[С₅С_х2]

Треугольник А₅В₅С₅-натуральная величина треугольник а АВС.

Пример 3. Определить точку пересечения прямой МЕ с плоскостью общего положения, заданной треугольником АВС.

Последовательность решения задачи на рисунке 78.

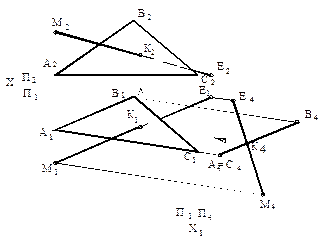
Рисунок 78

Так как прямая ВС является горизонталью, то вспомогательная плоскость П₄ проводится перпендикулярно П₁, а новая ось Х₁ будет перпендикулярна горизонтальной проекции горизонтали В₁С₁. Плоскость АВС станет проецирующей относительно плоскости П₄ и проецируется на нее в прямую линию А₄В₄С₄. Поэтому проекция точки К₄ искомой точки пересечения прямой МЕ с плоскостью АВС будет находиться на проекции А₄В₄С₄ или ее продолжении. Обратный переход от системы П₁/П₄ к исходной системе П₁/П₂ позволяет определить проекции К₁ и К₂ точки пересечения прямой МЕ с плоскостью АВС. Относительная видимость прямой и плоскости определяется методом конкурирующих точек.

Дата добавления: 2014-01-11