Метод вращения

Сущность метода вращения заключается в том, что плоскости проекций остаются неподвижными, а меняется положение объекта проецирования путем вращения вокруг неподвижной оси до удобного положения для проведения необходимых построений.

Если ось вращения не задана, ее располагают перпендикулярно к одной из плоскостей проекций, так как упрощаются все построения при решении задач.

Действительно, если ось вращения перпендикулярна к какой – либо плоскости проекций, то плоскость, в которой вращается точка, параллельна этой плоскости проекций. Траектория движения точки на эту плоскость проекций проецируется без искажения, а на вторую плоскость проекций проецируется в виде отрезка прямой линии.

Вращение вокруг оси, перпендикулярной плоскости проекций

Рассмотрим этот метод на примере (рисунок 79) поворота точки А вокруг оси i, перпендикулярной плоскости П₁, на некоторый угол. Траектория перемещения точки – окружность, плоскость которой перпендикулярна оси i и параллельна плоскости П₁. Поэтому на плоскость П₁ проецируется без искажения. Фронтальная проекция этой траектории будет прямая, параллельная оси Х. Точка О является центром вращения точки А, а отрезок А₁О₁=А₁^/О₁ – радиус вращения.

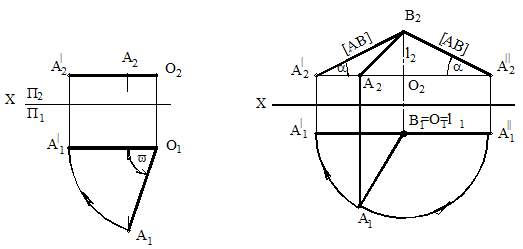
Рисунок 79 Рисунок 80

Пример. Определить длину отрезка АВ и угол наклона его к горизонтальной плоскости проекций П₁ (рисунок 80).

Ось вращения i проходит через точку В и перпендикулярна П₁. Вращая отрезок АВ вокруг оси i, в положение параллельное фронтальной плоскости проекций П₂, позволяет спроецировать отрезок на эту плоскость без искажения. При вращении точка А перемещается по дуге в плоскости, параллельной плоскости П₁ до положения пока А₁^/В₁ станет параллельно оси Х. При этом фронтальная проекция А₂ перемещается по прямой А₂А₂^/ параллельной оси Х. Отрезок [АВ]=[А₂^/В₂].

Вращение вокруг линии уровня

Форму плоской фигуры, занимающей общее положение относительно плоскостей проекций, можно определить поворотом вокруг ее горизонтали (или фронтали) в положение, параллельное соответствующей плоскости проекций. На рисунке 81 показано вращение точки А вокруг горизонтальной прямой MN до тех пор, пока точка А не окажется в плоскости, параллельной плоскости проекций П₁ и определяемой этой точкой и осью вращения.

При вращении вокруг горизонтальной прямой MN точка перемещается по дуге радиуса ОA₀, лежащей в плоскости Р, перпендикулярной к оси вращения. Когда точка A займет нужное положение A₁, горизонтальная проекция радиуса вращения (ОА₁^/) будет равна его истинной величине, которая может быть определена способом прямоугольного треугольника.

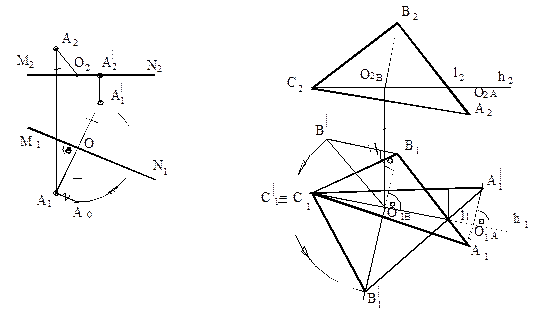
Рисунок 81 Рисунок 82

Пример. Определить истинную величину треугольника АВС (рисунок 82).

Возьмем в качестве оси вращения горизонталь C1(h₁). Так как ось вращения параллельна плоскости П₁, траектории перемещения вершин А и В будут проецироваться на эту плоскость в виде прямых, перпендикулярных проекции С₁1₁.Точки О_А и О_В пересечения плоскостей этих траекторий с осью С1(h₁) являются центрами вращения соответствующих вершин треугольника. Радиусы вращения точек А и В в исходном положении проецируются на плоскости П₁ и П₂ с искажением. Когда плоскость АВС в результате поворота займет горизонтальное положение, радиусы ВО_В и АО_А спроецируются на плоскость П₁ в истинную величину.

На рисунке 82 для построения проекции А₁^/В₁^/С₁^/ треугольника в горизонтальном положении, достаточно любым способом найти истинную величину радиуса ВО_1В или АО_1А и отложить ее на горизонтальной проекции траектории перемещения соответствующей вершины. В примере истинная величина радиуса вращения ВО равна В^/O_1В.

О_1ВВ^/ найдена способом прямоугольного треугольника и этим радиусом отложено расстояние от оси вращения до нового положения вершины В₁^/. Сторона А₁^/В₁^/ проведена из вершины В₁^/ через 1₁ до пересечения с горизонтальной проекцией плоскости вращения точки А. А₁^/ В₁^/С₁^/ – истинная величина треугольника АВС.

Дата добавления: 2014-01-11