Пересечение поверхностей плоскостью

При пересечении геометрических тел плоскостью получается плоская фигура, называемая сечением. В сечении многогранника плоскостью получается плоская фигура – многоугольник, а в сечении кривой поверхности – плоская кривая линия. Для построения контура сечения многогранника строят точки пересечения всех его ребер с плоскостью, получая вершины многоугольника. Для построения линии сечения кривой поверхности с плоскостью определяют точки пересечения ряда образующих поверхности с плоскостью, которые затем соединяют плавной кривой.

Таким образом, задачи на пересечение поверхностей плоскостью сводится к многократному решению задачи на пересечение прямой или кривой линии с плоскостью.

Рассмотрим несколько примеров.

На рисунке 102 показано построение фигуры сечения наклонной трехгранной призмы фронтально проецирующей плоскостью Р(Р₂).

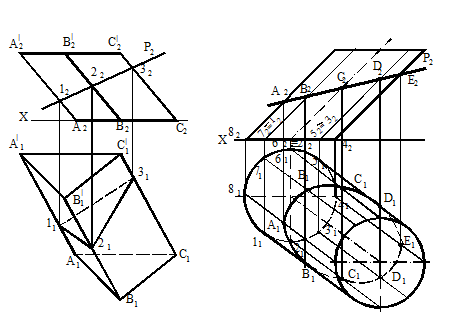
Рисунок 102 Рисунок 103

Так как плоскость Р - фронтально проецирующая, то фронтальная проекция сечения призмы плоскостью совпадает со следом плоскости Р₂. Точки 1₂, 2₂, 3₂ – фронтальные проекции точек пересечения ребер призмы с плоскостью Р. Горизонтальные проекции точек 1₁, 2₁, 3₁ определяются по принадлежности их соответствующим ребрам призмы.

На рисунке 103 показано построение сечения наклонного кругового цилиндра фронтально проецирующей плоскостью Р (Р₂).

На поверхности цилиндра проведены восемь образующих линий. Фронтальная проекция сечения определяется точками пересечения образующих с плоскостью Р и совпадает со следом Р₂, так как плоскость Р перпендикулярна плоскости П₂. Горизонтальная проекция сечения определяется по принадлежности точек сечения соответствующим образующим.

На рисунке 104 показаны линии пересечения прямого кругового конуса плоскостью Р (Р₂). Плоскость Р, перпендикулярная к оси конуса, пересекает поверхность конуса по окружности радиуса R.

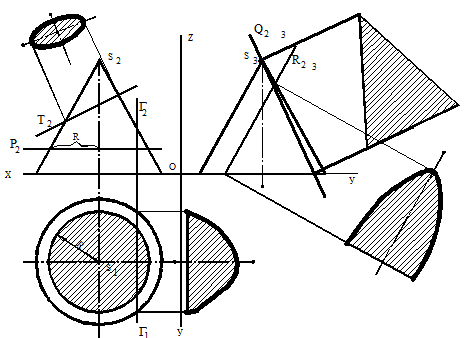
Рисунок 104

Плоскость Г (Г1; Г₂), параллельная двум образующим конуса, пересекает его поверхность по гиперболе. Плоскость Т (Т₂) пересекает поверхность конуса по эллипсу, т. к. она пересекает все образующие; плоскость R (R₂) параллельная образующей - по параболе. Плоскость Q (Q₂), проходящая через вершину конуса, пересекает его поверхность по образующим: фигура сечения - треугольник.

Рисунок 105

На рисунке 105 дано построение сечения прямого кругового цилиндра с плоскостью Р.

Горизонтальная проекция сечения совпадает с горизонтальной проекцией цилиндра, так как цилиндр является горизонтально проецирующей поверхностью. Фронтальные проекции точек сечения строятся по горизонтальным проекциям и по принадлежности точек сечения плоскости Р. Малая ось эллипса является его горизонталью, большая ось перпендикулярна малой. Большая ось эллипса 8 - 4 (точка 8 – низшая точка сечения, а 4 - высшая) определяется с помощью горизонтально проецирующей плоскости Г, проходящей через ось цилиндра и перпендикулярно плоскости Р. Малая ось эллипса ограничена точками 2 и 6, найденными с помощью вспомогательной горизонтали, расположенной в плоскости Р, проведенной через ось вращения цилиндра параллельно плоскости Р (на чертеже параллельно следу Р₁).

На рисунке 106 построены проекции сечения треугольной пирамиды плоскостью общего положения, заданной следами.

Основание пирамиды и горизонтальный след Р₁ расположены на плоскости П₁. Поэтому горизонтальные проекции точек 1₁ и 2₁ определятся на пересечении следа Р₁ с треугольником А₁В₁С₁. Фронтальная проекция точек 1₂ и 2₂ лежат на оси Х. Проекции точек 3 и 4 определяются как

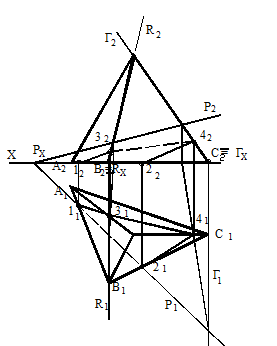
Рисунок 106

точки пересечения ребер АC и ВC с плоскостью Р. Соединив соответствующие проекции точек, получим проекции многоугольника - сечения пирамиды плоскостью.

Рисунок 107

На рисунке 107 дано построение сечения прямого кругового конуса плоскостью общего положения. Поскольку основание конуса расположено в горизонтальной плоскости проекций, проекции точек 1₁ и 2₁ определяются на пересечении горизонтального следа плоскости Р₁ с основанием конуса. Фронтальные проекции 1₂ и 2₂ находятся по линиям связи на оси Х. Далее задача сводится к определению точек пересечения ряда образующих с плоскостью Р. Точка 4 (наивысшая для сечения) определена с помощью ввода вспомогательной плоскости Г, перпендикулярной плоскости П₁, проходящей через вершину конуса и перпендикулярно плоскости Р (на чертеже Г₁ перпендикулярно следу Р₁). Для определения точек 3 и 5 (расположенных на очерковых образующих конуса) введены плоскости R и Ф.Для определения точек 2 и 6 введена плоскость Q, перпендикулярная П₁ и проходящая через образующие, горизонтальные проекции которых параллельны горизонтальному следу плоскости Р₁.

Подобные задачи решаются проще, если секущие плоскости преобразовать в проецирующие.

Рисунок 108

Например, на рисунке 108, для построения сечения поверхности трехгранной призмы плоскостью, общего положения Р, выполнена перемена плоскостей проекций и плоскость Р преобразована в проецирующую относительно плоскости П₄. Проекции призмы на плоскости П₄ определятся на пересечении ребер призмы А₄А₄^/, В₄В₄^/, С₄С₄^/ со следом Р₄, так как плоскость Р перпендикулярна плоскости П₄. Горизонтальная и фронтальная проекции точек сечения находятся по линиям связи на соответствующих ребрах призмы.

Дата добавления: 2014-01-11