Частный случай пересечения

Пересечение поверхностей вращения

Если одна из двух пересекающихся поверхностей является проецирующей, прямолинейные образующие этой поверхности (цилиндра, призмы) перпендикулярны одной из плоскостей проекций, то и проекции линии пересечения на эту плоскость определяется без дополнительных построений.

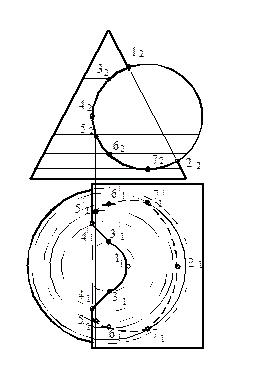На рисунке 124 показано построение линии пересечения конуса вращения с прямым круговым цилиндром.

Фронтальная проекция линии пересечения (проекции точек 1₂,2₂,3₂,4₂,5₂,6₂,7₂) определяется по принадлежности точек поверхности цилиндра. Горизонтальная проекция линии пересечения определяется из условия принадлежности ее поверхности конуса. Для построения горизонтальных проекций точек (1₁,2₂,3₁,4₁,5₁,6_1,7₁), на поверхности конуса проведены параллели через проекции точек, 3₂,4₂,5₂, 6_2, 7_2, а проекции точек 1₁ и 2₁ определены по принадлежности очерковой образующей конуса.

Рисунок 124

Дата добавления: 2014-01-11