Способ вспомогательных секущих плоскостей

Общий случай пересечения

В общем случае, для построения линии пересечения поверхностей, применяются:

- способ вспомогательных секущих плоскостей, если оси поверхностей не пересекаются;

- способ вспомогательных секущих сфер, если оси поверхностей пересекаются;

Этот способ применяется для построения линии пересечения поверхностей, когда плоскости рассекают пересекающиеся поверхности по графически простым линиям – прямым или окружностям. На рисунок 125 приведен пример построения линии пересечения поверхности конуса с поверхностью сферы этим способом.

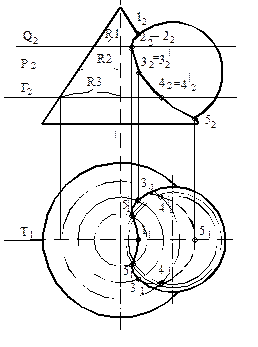
Рисунок 125

Конус – прямой круговой и его основание параллельно горизонтальной плоскости проекций. Точки 1 и 5 определяются без дополнительных построений по принадлежности их очерковым образующим обеих поверхностей. Для нахождения проекций точек 3, 3^/ , 2, 2^/ и 4, 4^/ проведены вспомогательные горизонтальные секущие плоскости Р(Р₂), Q(Q₂) и Г(Г₂). Плоскость Р проведена через центр сферы, благодаря чему получены проекции точек 3 и 3^/- характерных точек, определяющих границу видимости линии пересечения на горизонтальной проекции. Секущие плоскости Р, Q и Г рассекают обе поверхности по окружностям радиусов R1, R2 и R3, плоскости которых параллельны горизонтальной плоскости проекций. Горизонтальные проекции точек 3₁, 3^/₁, 2, 2^/ и 4₁, 4^/₁ определены в точках пересечения соответствующих окружностей. Фронтальные проекции найдены по линиям связи на следах плоскостей Р₂ и Г₂. Полученные точки 1, 2, 3, 4 и 5 последовательно соединены с учетом видимости на каждой проекции.

На рисунок 126 показано определение линии пересечения этих же поверхностей, но со смещением осей вращения относительно фронтальной плоскости проекций на разное расстояние. В этом случае, для определения опорных точек 1 и 5, требуются дополнительные построения. Одним из способов преобразования чертежа приводится положение поверхностей к такому, как показано на рисунок 125. Для этого, через вершины поверхностей проводится вспомогательная секущая плоскость Т (Т₁).

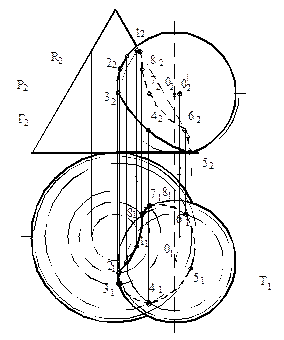
Рисунок 126

Строятся истинные величины сечения (в данном примере методом вращения вокруг оси перпендикулярной П₁ и проходящей через ось вращения конуса) на фронтальной плоскости проекций. Истинная величина сечения конуса плоскостью Т будет треугольник, совпадающий с проекцией самого конуса. Истинная величина сечения сферы плоскостью Т будет окружность, диаметр которой равен диаметру сферы. В пересечении фронтальных проекций сечений конуса с сечением сферы получены фронтальные проекции параллелей опорных точек 1 и 5. Горизонтальные проекции точек 1₁ и 5₁ определятся в пересечении горизонтальных проекций параллелей конуса со следом плоскости Т₁. Фронтальные проекции 1₂ и 2₂ определены по линиям связи на соответствующей параллели конуса. Промежуточные точки 3, 4, 5, 6 построены с помощью горизонтальных секущих плоскостей R(R₂), Р(Р₂) и Г(Г₂). Соединены плавной линией горизонтальные проекции точек 1₁, 2₁, 3₁, 4₁, 5₁, 6_1, 7₁, 8₁ и фронтальные проекции точек 1₂, 2₂, 3₂, 4₂, 5₂, 6₂, 7₂, 8₂,учитывая их видимость на поверхностях конуса и сферы. Получена линия пересечения заданных поверхностей. Показана видимость самих поверхностей.

Дата добавления: 2014-01-11