Изменение энтропии в неизолированных системах

В неравновесных системах также протекают необратимые процессы и, следовательно, производится энтропия. Но в отличие от изолированных систем в них энтропия не накапливается, а отводится в окружающую среду. Этот отток энтропии обеспечивает диссипацию - необратимый переход части энергии упорядоченных процессов в энергию неупорядоченных процессов. Изменение энтропии в такой системе dS складывается из производства энтропии внутри системы за счет эффектов необратимости d_iS и из переноса (потока) энтропии через границу системы d_eS (здесь индекс «е» означает «вне» - «exstra»):

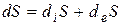(5.12)

В уравнении (5.12) производство энтропии всегда положительно: d_iS > 0. Поток энтропии либо отрицателен d_eS < 0, (система выделят энтропию в окружающую среду), либо положителен d_e S > 0, (энтропия поступают в систему извне) (рис. 5.2).

Если энтропия отводится от системы, то возможны следующие ситуации.

При

(5.13)

система асимптотично (бесконечно) стремится к равновесию, и процесс постепенно затухает.

При

(5.14)

dS = 0 (5.15)

устанавливается стационарное состояние (стационарный процесс), в котором степень упорядочения системы остается неизменной.

Поток

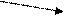
d_eS

внешняя

среда

Рис. 5.2. Система, в которой d_iS означает производство энтропии,

а d_eS – обмен энтропией между системой и окружающей средой.

Если диссипация слишком велика, и величина потока энтропии по модулю превышает величину производства энтропии

, (5.16)

то изменение энтропии системы будет отрицательно

. (5.17)

Тогда из (4.17) следует, что без нарушения второго начала термодинамики (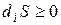) в открытой системе энтропия уменьшается, т.е. уменьшается беспорядок. Эта ситуация возможна только в открытых системах, т.е. открытая система может сама формировать новую, более упорядоченную структуру за счет оттока энтропии в окружающую среду (усиления диссипации). Приведем пример. Экономическая система – фирма - производит товар (энтропию), который она успешно реализует на рынке, осуществляются направленные изменения: товар производится и «уходит», что обеспечивает капитал восстановления (энтропия отводится из системы). В результате, если восстанавливающийся капитал равен затратам, фирма работает стабильно в стационарном ритме. Если вырученный капитал выше затраченного (модуль отрицательного потока энтропии превышает модуль положительного при производстве товара), фирма за счет прибыли имеет возможность повышать качество товара, расширять его ассортимент и т.п. путем совершенствования старой или внедрения новой технологии. Тем самым она улучшает свою структуру, укрепляет порядок (уменьшает энтропию).

Заметим, что открытая система не может быть равновесной, так как ее функционирование требует непрерывного поступления из внешней среды вещества и энергии.

В динамике тепловых процессов важно не значение энтропии S и даже не изменение энтропии dS, а скорость изменения энтропии. Поэтому соотношение (5.12) можно представить в следующем виде:

, (5.18)

где - скорость изменения энтропии неизолированной системы, - скорость производства энтропии внутри системы, - скорость переноса энтропии через границу системы.

Важным фактором, определяющим состояние системы, является скорость производства энтропии. Рассмотрим неравновесный процесс, который моделирует большой круг явлений в различных областях: в пленочных биосистемах с мембранами, гидропотоках с фильтрами, слабонеравновесных экономических системах и др. Пусть система состоит из двух камер, соединенных пористой стенкой (рис. 5.3). Неравновесность поддерживается разностью температур, которая вызывает тепловой поток (1) и термодиффузионный поток массы (2). Со временем возникшая разность концентраций молекул создает встречный диффузионный поток массы (3) и компенсирует поток массы (2). В результате в системе остается один поток тепла (1) и возникает неравновесное стационарное состояние. В таких состояниях энтропия системы не меняется со временем. Количественно устойчивость стационарного состояния определяется теоремой И.Р. Пригожина (1917 – 2003): в любой закрытой или открытой системе, переходящей в неравновесное стационарное состояние, скорость производства энтропии достигает минимального значения.

Рис. 5.3 Возникновение неравновесного стационарного состояния в системе

с T₁>T₂. Со временем остается лишь один поток тепла (1). Поток массы

из-за ΔТ (2) компенсируется встречным потоком массы (3), вызванным

концентрационным градиентом.

Стационарное состояние в неизолированных системах является аналогом равновесного состояния изолированных систем. Это состояние, в котором параметры системы остаются неизменными сколь угодно долго. Стационарность – более общее понятие по сравнению с равновесностью, которая является частным случаем стационарности. В стационарном состоянии параметры в разных частях системы могут быть разными, т.е. может иметь место неравновесие и это неравновесие сохраняется. Как указано выше, условие возникновения стационарного состояния открытой системы – минимум скорости производства энтропии . Математически это означает равенство нулю второй производной:

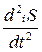= 0. (5.19)

При этом реализуются условия (5.14) и (5.15). Энтропия системы остается постоянной, хотя и не максимальной, как в равновесном состоянии. Стационарное состояние характеризуется почти теми же особенностями, что и равновесное. Однако это более упорядоченное состояние, и данный порядок сохраняется.

Теорему И.Р. Пригожина успешно используют для описания процессов «слабо неравновесного» рынка товаров, а также «сильно неравновесного» рынка. Можно увязать (сопоставить) с этой теоремой утверждение, что полезность произведенного товара в каждый предыдущий момент времени выше, чем в последующий. Читателю предлагается сделать это самостоятельно.

Центральная роль в динамике неравновесных процессов принадлежит потокам и движущим силам. Как установил Л. Онсагер, они определяют скорость изменения энтропии . Пусть в системе сила X_i создает поток I_i, а извне на систему действует сила X_е и вызывает поток I_e. Теорема Онсагера гласит: скорость изменения энтропии открытой системы равна алгебраической сумме произведений потоков на соответствующие обобщенные силы, действующие в системе и на систему.

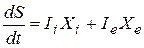. (5.20)

Например, рассмотрим экономическую систему (фирма, предприятие), в которой символ i определяет процесс предложения, а параметры I_i, X_i соответственно - поток выпущенного товара и его себестоимость, а символ е – процесс спроса, параметры I_e, X_e соответственно спрос на товар и цена его на рынке. Тогда уравнение (5.20) устанавливает связь между спросом и предложением, которая представлена кривыми спроса и предложения в курсе экономической теории. Важно отметить, что каждый из параметров I_i и I_e в (5.20) зависит от обеих обобщенных сил X_i и X_e, т.е. I_i (X_i, X_e) и I_e (X_i, X_e), чем в частности, обеспечивается связь между спросом и предложением.

Дата добавления: 2014-01-11