Виды дисперсии. Правило сложения дисперсий

I. ()

Понятие о вариации. Показатели вариации

При изучении статистических совокупностей наряду со средними величинами большое практическое значение имеет изучение вариации признака. Для измерения и оценки вариации используются абсолютные и относительные показатели вариации: размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение, каэффициент вариации и др.

Результаты сдачи экзамена по микроэкономике:

Оценка (варианты)	Число студентов (частоты)
Итого

II. ()

Распределние студентов 2 курса КЭФ по количеству пропущенных занятий:

Группы студентов по количеству пропусков, часов	Число студен-тов, чел.
до 26
26-52
52-78
78-104
104-130
130 и выше
Всего

Размах вариации () характеризует диапазон вариации и исчисляется как разность между максимальным (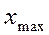) и минимальным () значением признака:

.

Среднее линейное отклонение (Л) представляет собой среднюю арифметическую из абсолютных значений отклонений отдельных вариантов от их средней арифметической:

I. (для ряда чисел, т.е. для несгруппированных данных)

II. 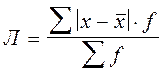(для вариационного ряда, т.е. для сгруппированных

данных)

Дисперсия () представляет собой средний квадрат отклонений вариантов от их средней арифметической:

I. 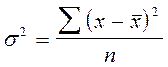(для ряда чисел)

II. (для вариационного ряда)

Для исчисления дисперсии используются упрощенные способы расчета:

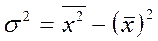; , где

- средняя арифметическая квадратов условных вариант;

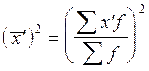- квадрат средней арифметической условных вариант;

- средняя арифметическая квадратов вариантов;

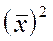- квадрат средней арифметической.

Среднее квадратическое отклонение () характеризует меру абсолютной колеблемости признака относительно средней величины и равно корню квадратному из дисперсии:

I. 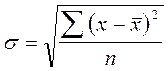(для ряда чисел)

II. (для вариационного ряда)

Коэффициент вариации () характеризует относительную колеблемость значений признака относительно средней и представляет собой выраженное в процентах (или в виде доли) отношение среднего линейного или среднего квадратического отклонения к средней величине:

; .

Если статистическая совокупность разбита на группы по какому-либо признаку, то для такой совокупности могут быть исчислены дисперсии: общая, групповые (внутригрупповые), средняя из групповых, межгрупповая.

Общая дисперсия () измеряет вариацию признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию, и вычисляется по одной из формул, приведенных выше.

Внутригрупповые дисперсии (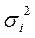) показывают величину вариации в каждой группе, обусловленную всеми факторами, кроме фактора, положенного в основу группировки:

Средняя из групповых дисперсий (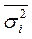)отражает вариацию, обусловленную всеми факторами, кроме фактора, положенного в основу группировки, но в среднем по совокупности:

.

Межгрупповая дисперсия () характеризует вариацию групповых средних, обусловленную влиянием группировочного признака:

Общая дисперсия равна сумме средней из групповых дисперсий и межгрупповой дисперсии. Это правило сложения дисперсий:

.

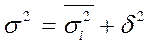Отношение межгрупповой дисперсии к общей показывает, какая часть общей вариации изучаемого признака обусловлена вариацией группировочного признака и носит название эмпирического коэффициента детерминации:

.

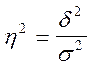Для оценки тесноты связи между группировочным и результативным признаком исчисляется эмпирическое корреляционное отношение:

.

.

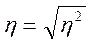Дата добавления: 2014-01-11