Понятие функции

Пусть Х и У – некоторые множества.

Опр. Если каждому элементу 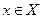ставится в соответствие по некоторому правилу единственный элемент 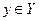, то говорят, что на множестве Х задана функция (функциональная зависимость) со значениями в множестве У:

, .

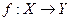Множество Х называется областью определения функции и обозначается D(f), множество У называется областью значений функции и обозначается I(f).

В мат. анализе рассматривают в основном числовые функции, т.е. такие, где Х и У – множества действительных чисел.

Если функция f переводит элемент 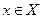в элемент 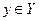, то х называют независимой переменной или аргументом или прообразом элемента у, у называют зависимой переменной или значением функции или образом элемента х. Для функциональной зависимости образ всегда единственен.

Способы задания функций (задать множества и описать правило):

- аналитический, с помощью одной или нескольких формул:

- табличный:

Год
Численность населения (млрд)

- графический (ЭКГ);

- словесный (функция Дирихле 1-рац., 0-иррац.);

- (читается «у равно антье х») целая часть – наибольшее число, не превосходящее х.

Например, .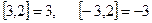

Функция называется явной, если она задана формулой, разрешенной относительно зависимой переменной. Если функция задана уравнением, не разрешенным относительно зависимой переменной, то говорят, что функция задана неявно.

()

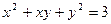Опр. Композицией отображени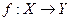й и 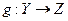называется отображение .

Например, ;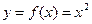

;

.

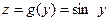Композицию числовых функций называют сложной функцией или функцией от функции.

Опр. Если обратное соответствие, переводящее Y в X является функцией, т.е. у каждого элемента 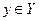имеется единственный прообраз 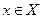, то это соответствие называют обратным отображением или обратной функцией к функции :

, .

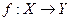Пример. Рассмотрим функцию 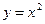при x0.

Выразим х: , . Обратной функцией будет являться .

Т.к. традиционно независимую переменную обозначают х, то, переобозначив переменные, получим обратную функцию .

Обратная функция к обратной функции совпадает с исходной функцией: .

Обратная функция существует для любой строго монотонной функции.

Опр. Графиком числовой функции y=f(x) называется совокупность точек плоскости вида (x,f(x)), где .

Графики обратных функций симметричны относительно биссектрисы I и III координатных углов.

Некоторые свойства функций.

Опр. Числовая функция y=f(x) называется монотонно возрастающей (убывающей), если большему значению аргумента соответствует большее (меньшее) значение функции:

.

Опр. Числовая функция y=f(x) называется ограниченной сверху на множестве А, если найдется число М такое, что:

.

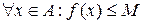Опр. Числовая функция y=f(x) называется ограниченной снизу на множестве А, если найдется число М такое, что:

.

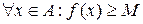Опр. Числовая функция y=f(x) называется ограниченной на множестве А, если найдется число К такое, что:

.

В противном случае функция называется неограниченной.

Числовая функция y=f(x) называется четной, если 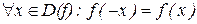; числовая функция называется нечетной, если .

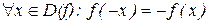Числовая функция y=f(x) называется периодической, если найдется такое число Т>0, что .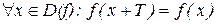

Элементарные функции и их классификация.

К основным элементарным функциям относят: линейную, степенную, показательную, логарифмическую, тригонометрические и обратные тригонометрические функции.

Опр. Функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий и/или конечного числа операций образования сложной функции, называются элементарными.

Пример. Неэлементарные: .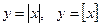

Элементарные функции делят на алгебраические и трансцендентные.

Алгебраической называется функция, в которой над аргументом проводится конечное число алгебраических действий (например, полином, дробно-рациональная функция, иррациональная функция). Остальные – трансцендентные (показательная, логарифмическая, тригонометрические и обратные тригонометрические функции).

Знать свойства и графики основных элементарных функций.

Преобразования графиков функций

1. 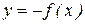- симметричное отображение относительно оси О х.

2. - симметричное отображение относительно оси О у.

3. - параллельный перенос на а влево/ вправо.

4. - параллельный перенос на а вверх/ вниз.

5. - растяжение (для к>1) /сжатие (для 0<к<1) в к раз вдоль оси О у.

6. 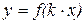- растяжение (для 0<к<1) /сжатие (для к>1) в к раз вдоль оси О х.

7. 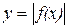- часть графика, расположенная ниже оси Ох, отображается симметрично относительно оси О х, остальная часть графика не изменяется.

8. - часть графика, расположенная в правой полуплоскости копируется в левую полуплоскость.

Дата добавления: 2014-01-13