Метод множителей Лагранжа. Пусть точка есть точка условного экстремума функции при наличии двух уравнений связи

Пусть точка 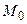есть точка условного экстремума функции 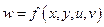при наличии двух уравнений связи

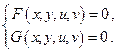
Если якобиан 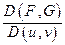отличен от нуля, то система двух уравнений связи теоретически определяет две функции 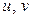от аргументов 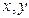: 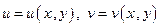. Тогда

а) функция имеет экстремум в точке и в силу следствия из теоремы в этой точке

б) из уравнений связи имеем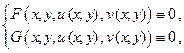

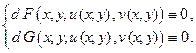
Воспользовавшись свойством инвариантности первого дифференциала, запишем:

Умножим второе уравнение на множитель 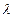, третье уравнение – на множитель 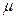и сложим с первым уравнением: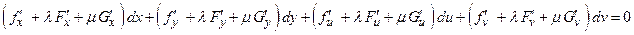

Введем функцию Лагранжа 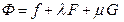(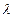и 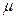называют множителями Лагранжа) и запишем предыдущее равенство с помощью этой функции:

.

Выберем 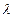и 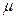так, чтобы 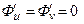. Это возможно, так как система уравнений

имеет единственное решение в силу того, что определитель системы .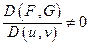

С учетом равенства 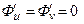соотношение примет вид 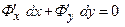. Это равенство верно при любых и ;

в частности, при 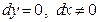из равенства получим ,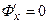

при из равенства 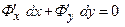получим .

Итак, в точке экстремума .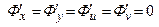

Для отыскания условного экстремума

функции 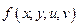при наличии уравнений связи нужно:

1) составить вспомогательную функцию Лагранжа следующим образом:

;

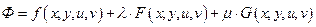2) найти ее критические точки из уравнений и уравнений связи ;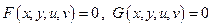

3) исследовать критические точки на экстремум, исходя из геометрических или физических соображений или знака .

Аналогично этот метод применяется и для отыскания экстремума функции 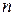переменных при наличии уравнений связи .

Дата добавления: 2014-01-13