Общая постановка задачи. Условный экстремум функции

Условный экстремум функции

Требуется найти экстремум функции на поверхности с уравнением 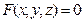или на линии заданной пересечением двух поверхностей.

Исследовать функцию 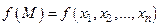на экстремум при наличии уравнений связи

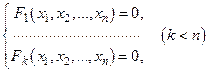. (18.5)

Точку 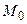назовем точкой условного минимума (соответственно, максимума) функции 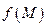при наличии связей (18.5), если 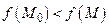(соответственно, 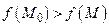) для всех точек 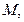принадлежащих некоторой окрестности точки 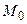и удовлетворяющих уравнениям связи (18.5).

Для краткости записи ограничимся случаем экстремума функции 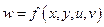четырех переменных при наличии двух уравнений связи

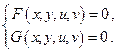
Будем предполагать, что якобиан 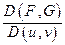отличен от нуля. Тогда система двух уравнений теоретически определяет две функции 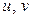от аргументов :

.

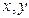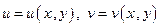В зависимости от того, можно ли практически выразить 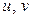из системы уравнений (5.3), различают два метода отыскания условного экстремума.

Дата добавления: 2014-01-13