
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 7. Эластичность спроса и предложения
|
|
|
|
РАЗДЕЛ 0. У БАРБОСА ЕСТЬ ВОПРОСЫ. Упрямые и покладистые покупатели
ИГОРЬ. Антон, ты помнишь определение эластичности, которое мы прочли в статье Эджуорта, написанной для первого издания словаря Пэлгрэйва?
АНТОН. Да, да, вспоминаю. Это те несколько больших томов издания 1901 г., которые хранятся в нашей библиотеке с неразрезанными страницами.
ИГОРЬ. Так вот, Эджуорт пишет, что эластичность - технический термин, использованный Маршаллом для обозначения чувствительности реакции одного фактора в результате воздействия на него другого фактора.
АНТОН. Если ты, например, хочешь понять, как я изменю свой спрос на яблоки, если они подорожают на 10 %, то достаточно ли сказать, что я стану покупать их на 15% меньше, чем до увеличения цены?
ИГОРЬ. Конечно, ты в данном случае чувствительно реагируешь, т. е. цена повысилась только на 10 %, а ты уменьшил спрос на 15 %.
АНТОН. Но если, скажем, я был бы менее покладистым и более упрямым хотя бы потому, что очень люблю яблоки?
ИГОРЬ. Естественно, такое вполне возможно. Часто можно наблюдать, как люди не хотят отказываться от своих вкусов и привычек.
БАРБОС. Не только люди, собаки тоже очень не любят отказываться от своих привычек.
АНТОН. А если, предположим, я стал покупать яблок меньше на 1 %, когда цена на яблоки поднялась на 10%?
ИГОРЬ. Тогда коэффициент эластичности будет равен одной десятой и твой спрос считается неэластичным, т. е. жестким. Или, как ты только что сказал, ты упрямишься, настаиваешь на сохранении прежних привычек.
АНТОН. Так, так, я понял. Если я реагирую бурно на изменение цены и спрос уменьшается на большее число процентов, чем то число процентов, на которое увеличивается цена, то коэффициент эластичности будет больше единицы и спрос называется эластичным, а если я реагирую сдержанно, изменяя спрос на меньшее число процентов, чем изменилась цена, то мой спрос неэластичный.
ИГОРЬ. Но чувствительность на изменение цены у каждого человека зависит не только от его характера, привычек, но и от того, есть ли у этого товара заменитель.
АНТОН. Но об этом мы будем рассказывать в лекции 7. Сейчас давай приведем пример с солью.
ИГОРЬ. Хорошо. Если цена на соль повыситься, то реакция спроса практически у каждого будет жесткой, а коэффициент эластичности будет близок к нулю именно потому, что соль нечем заменить.
БАРБОС. Тут поневоле будешь упрямым, а не покладистым.
АНТОН. Нужно еще сказать, что чувствительность людей с разным доходом будет тоже разной.
ИГОРЬ. Понятно, что у более состоятельных покупателей есть больше возможностей поупрямиться и сохранить свои привычки.
АНТОН. Еще обязательно нужно сказать, что эластичность можно измерять не только для спроса по цене, но и по доходу, например.
ИГОРЬ. Эта тема очень интересна для наших читателей. Каждый знает, что есть товары, которые мы. покупаем все больше, если наш доход возрастает. Но есть товары, которые мы покупаем все меньше, если наш доход возрастает.
АНТОН. Ты забыл привести пример. В первом случае, скажем, фрукты, овощи, жилье, путешествия и т. д. Во втором - хлебобулочные изделия, картофель, маргарин.
ИГОРЬ. Все верно. Подробно об этом мы будем рассуждать во второй части. А здесь можно обратить внимание читателя на то, что можно измерять эластичность и предложения, например, в результате повышения цены.
АНТОН. Думаю, все уже поняли, что чувствительность, или эластичность, - очень интересное свойство, и изучать его полезно применительно и к спросу, и к предложению, в зависимости от самых разных факторов.
РАЗДЕЛ 1. Что показывает эластичность
Функция спроса Q = D(P) устанавливает зависимость объема спроса Q от цены P. Главный вопрос, возникающий при анализе этой зависимости, - это вопрос о том, насколько резко изменится объем спроса при том или ином изменении цены.
Обычно степень влияния одной переменной на другую, зависимую от нее, измеряют производной соответствующей функции. Если ΔР - изменение цены, ΔQ - вызванное им изменение объема спроса, то значение производной покажет, на сколько единиц изменится спрос в расчете на единичное изменение цены в бесконечно малой окрестности исходного значения. Графически этому соответствует крутизна наклона касательной к кривой спроса по отношению к оси цен.
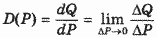 , (1) , (1)
|
Напомним читателю, что в экономической литературе принято откладывать объемы по горизонтальной оси, а цены - по вертикальной. Если в качестве аргумента рассматривается цена, а объем выступает в роли функции (как в настоящей лекции), читателю нужно иметь в виду, что оси аргумента и функции расположены непривычным образом.
Однако непосредственное использование производной как характеристики реакции спроса на изменение цен не дает ответа на ряд вопросов, интересующих экономиста. Пусть повышение цены за 1 кг картофеля на 10 коп. снижает годовой объем спроса на 10 кг, т. е. ΔР = 0.1 руб./кг, ΔQ = -10 кг/год (знак "минус" соответствует уменьшению). Считая эти изменения малыми, можно приближенно оценить производную:
 , ,
|
(обратите внимание на размерность!). Допустим, аналогичным образом мы установили, что для обуви:
 , ,
|
Какая из этих величин больше? Вопрос бессмыслен, и не только из-за того, что величины, измеренные в различных единицах, несопоставимы. Даже формальное совпадение единиц не разрешило бы трудности, так как 1 кг картофеля для потребителя не эквивалентен такому же количеству, скажем, чая.
Перечисленные (и иные) трудности можно преодолеть, если в качестве основного показателя реакции спроса на изменение цены использовать не производную, а эластичность спроса по цене - предел отношения относительного приращения объема δQ = ΔQ/Q к относительному приращению цены δР = ΔР / Р при условии, что последнее стремится к нулю:
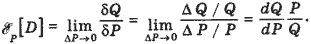 , (2) , (2)
|
При анализе относительных изменений эластичность играет примерно такую же роль, что производная - при анализе абсолютных изменений. Свойства этой характеристики зависимостей изложены в Математическом приложении (далее - МП), II.
Эластичность - безразмерная величина; ее использование снимает сложности, связанные с единицами и масштабами рассматриваемых величин. Эластичность и производная не связаны друг с другом однозначно, хотя и совпадают по знаку (поскольку Р и Q - положительные величины), и в одних и тех же случаях стремятся к нулю (когда реакция спроса на изменение цены отсутствует) или к бесконечности (когда потребитель "бесконечно сильно" реагирует на ничтожное изменение цены). Крутизна наклона кривой в общем случае не характеризует величину эластичности, ее геометрические свойства несколько менее наглядны.
В нормальных случаях с увеличением цены объем спроса уменьшается. Поэтому можно считать, что всегда Εp[D] < 0, и при анализе спроса знак эластичности не представляет интереса. Для измерения величины реакции спроса на изменение цены удобнее использовать абсолютную величину эластичности:
η = |Εp[D]|(3)
Некоторые авторы, чтобы иметь дело с положительными показателями, определяют эластичность потребления по спросу как:
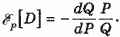 , (1) , (1)
|
Такое определение не соответствует общему определению эластичности функции.
Спрос называют неэластичным, если 0 < η < 1, и эластичным, если η > 1. Посмотрим, с какими реальными обстоятельствами связана эластичность спроса по цене (табл. 1; рис.1).
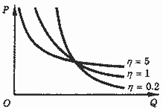
Рис. 1. Кривые спроса с низкой (=0.2), единичной (=1) и высокой (=5) эластичностью.
Таблица 1. Реакция покупателей на изменения цены
| η | Характер спроса | Поведение покупателей | |
| при снижении цены | при возрастании цены | ||
| η = ∞ | Совершенно эластичный | Повышают объем закупок на неограниченную величину | Снижают объем закупок на неограниченную величину (полностью отказываются от товара) |
| 1 < η < ∞ | Эластичный | Значительно повышают объем закупок (спрос растет более высоким темпом, чем снижается цена) | Значительно снижают объем закупок (спрос снижается более высоким темпом, чем растет цена) |
| η=1 | Единичная эластичность | Спрос растет в том же темпе, что и падает цена | Спрос снижается в том же темпе, что и растет цена |
| 0< η <1 | Неэластичный | Темп роста спроса меньше темпа снижения цены | Темп снижения спроса меньше темпа роста цены |
| η = 0 | Совершенно неэластичный | Совершенно не изменяется объем закупок | Совершенно не изменяется объем закупок |
1. Чем больше товаров, являющихся, с точки зрения покупателя, заменителями данного, тем эластичнее спрос. Например, спрос на мыло определенной марки. Если цена на эту марку мыла повысится, то большинство покупателей безболезненно перейдут на другие сорта, хотя кто-то, возможно, останется верен своей привычке (вот почему так важен оборот "с точки зрения покупателя" в первой фразе этого пункта). Другой пример - магнитофоны. Спрос на импортную аудиотехнику на черном рынке достаточно эластичен.
Однако представим себе, что подобные устройства вообще не выпускались бы в России. Думается, покупатели были бы более снисходительны.
Отсюда следует и такой вывод: чем более агрегированный товар мы рассматриваем, тем ниже эластичность. Так, спрос на мыло вообще малоэластичен (его заменить нечем), однако спрос на мыло "Консул" может иметь весьма высокую эластичность.
2. Чем выше доля расходов на данный товар в бюджете потребителя, тем выше эластичность. Если потребитель расходует на данный товар незначительную часть своего бюджета, ему не нужно изменять свои привычки и пристрастия при изменении цены. С этой точки зрения интересна история такого товара, как соль. Совершенная неэластичность спроса на соль отмечалась в разделе 0. Но так было не всегда. В середине XIX в. в России пуд соли стоил от 50 коп. до 1 руб. из-за высокого налога на соляное производство. Для многих, особенно в деревне, это было непомерно дорого. После отмены акцизного налога в 1880 г. цена соли упала в два раза, а потребление выросло на 70 %.
Но одна и та же сумма при большом доходе составила бы малую долю бюджета, а при низком доходе - значительную. Поэтому эластичность спроса на один и тот же товар у потребителей с высоким доходом меньше, чем с низким.
3. Эластичность спроса ниже всего у тех товаров, которые, с точки зрения потребителя, являются необходимыми. Речь тут идет не только о хлебе. Для одного необходимыми товарами являются табак и алкоголь, для другого - марки и спичечные этикетки, для третьего - джинсы "Levi Strauss". Это дело вкуса.
Разновидностью данной закономерности является особенно низкая эластичность спроса на те товары, потребление которых (опять-таки с точки зрения потребителя) не может быть отложено. "Мне очень нужно" плюс "мне срочно нужно" - и покупатель становится сговорчивым. Пример: спрос на цветы 8 марта, 1 сентября и т.п.
Ранее мы разделяли эластичность на высокую и низкую, сравнивая ее абсолютное значение с единицей. Значение η = 1 интересно во многих отношениях. Одна из его особенностей обнаруживается при анализе зависимости от цены суммарных расходов потребителей R(P) = PD(P) на приобретение данного товара.
Формула (5) (см. МП, II) показывает, что Εp[R] = Εp[D] + 1. Это значит, что при Εp[D] >-1 (т. е. при низкой эластичности, η < 1) затраты возрастают при увеличении цены, а при Εp[D] < -1 (т. е. при высокой эластичности, η > 1) - убывают: резкая реакция покупателей на возрастание цены приводит к сокращению объема спроса более значительному, чем вызвавшее его повышение цены.
Таблица 2. Общие расходы при изменениях цен
| Εp[D] | η | Характер спроса | dR/dP | Изменение общих расходов | |
| При уменьшении цены | При увеличении цены | ||||
| Εp[D]< -1 | >1 | Эластичный | <0 | Возрастают | Уменьшаются |
| Εp[D]=1 | =1 | Единичная эластичность | Не изменяются | Не изменяются | |
| Εp[D]> -1 | <1 | Неэластичный | >0 | Уменьшаются | Возрастают |
Постоянной эластичностью n = 1 обладает степенная функция с показателем степени - 1 (см. МП, II, формула (9) и упражнение 3), т. е. обратная пропорциональность D(P) = а / Р.
Непосредственно видно, что для такой функции спроса справедливо равенство:
R(P) = P·a/p = a,
т. е. суммарные расходы на приобретение товара не зависят от его цены.
Если эластичность спроса на товар - переменная величина, то суммарные расходы будут возрастающей функцией цены на участках с низкой эластичностью и убывающей - на участках с высокой эластичностью. Максимумам суммарных расходов (переходам от возрастания к убыванию) и минимумам (обратным переходам) соответствуют цены, при которых η = 1.
В качестве иллюстрации рассмотрим линейную функцию спроса (рис. 2,а).
Эта функция имеет постоянную производную, но ее эластичность изменяется во всем диапазоне возможных значений: когда цена стремится к нулю, эластичность также стремится к нулю, по мере приближения к цене P0 эластичность стремится к бесконечности. В середине этого интервала, т. е. при Р =P0 / 2, выполняется равенство η = 1 (см. МП, II, упражнение 1), и суммарные расходы принимают наибольшее значение. На рис. 2,б представлен график функции суммарных расходов R(P) и показано положение максимума.
Читатель может самостоятельно в качестве упражнения представить функцию спроса в аналитической форме и после необходимых выкладок убедиться в том, что суммарные расходы будут максимальными в указанной на рисунке точке.

Рис. 2. Линейная функция спроса (а) и функция суммарных расходов (б).
До сих пор мы интересовались зависимостью объема спроса на определенный товар от цены на этот товар. В действительности же спрос зависит от многих факторов. В качестве важнейших из них можно выделить цены на другие товары и доходы потребителей. При анализе зависимости спроса от этих факторов также широко используется аппарат эластичности.
Мерой реакции спроса на данный товар на изменение цены некоторого другого товара служит перекрестная (или взаимная) эластичность спроса по цене. Для ее определения может быть использована уже знакомая нам формула (1), с тем лишь отличием, что объем спроса (Q) относится к одному товару, а цена (Р) - к другому. Спрос на данный товар при увеличении цены на другой товар может и возрастать, и убывать - в зависимости от отношения потребителя к совместному использованию того и другого товара. Например, рост цены на бензин должен снижать спрос на автомобили; в то же время повышение цены на хозяйственное мыло увеличивает спрос на стиральный порошок. Таким образом, перекрестная эластичность может быть и положительной, и отрицательной, и ее знак представляет не меньший интерес, чем абсолютная величина. Первый пример относился к взаимодополняемым товарам; для них характерна отрицательная перекрестная эластичность. Во втором примере речь идет о взаимозамещаемых товарах; здесь мы обычно сталкиваемся с положительной перекрестной эластичностью. Теперь обратимся к эластичности спроса по доходам. Ее можно определить аналогично эластичности спроса по цене:
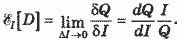 , (4) , (4)
|
Здесь Q - объем спроса на определенный товар, I - доход потребителя, символ δ, как и раньше, обозначает относительные приращения. Такие зависимости обычно изучают путем сопоставления спроса в группах потребителей, каждая из которых более или менее однородна по уровню дохода.
Рост дохода увеличивает возможность совершения покупок, так что спрос на большинство товаров с увеличением дохода возрастает, и эластичность спроса по доходам оказывается положительной. Но по абсолютной величине эти эластичности могут резко различаться. Эластичность спроса на товары первой необходимости весьма мала, а на предметы роскоши - велика. Кроме того, существуют товары, которые при достаточно высоком уровне доходов вытесняются лучшими товарами-заменителями, и спрос на них при дальнейшем увеличении дохода падает. На этом участке эластичность оказывается отрицательной. Такие товары называют низшими благами (рис. 3).

Рис. 3. Зависимости спроса (Q) от доходов (I). 1 - товары первой необходимости (ΕI <1); 2 - предметы роскоши (ΕI > 1); 3 - низшие блага (ΕI<0 при больших доходах).
Итак, мы видим, что такой показатель, как эластичность спроса, служит весьма полезным инструментом выявления отношения потребителей к различным товарам. Но этот же инструмент может быть использован и для анализа предложения.
Эластичность предложения по цене:
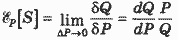 , (5) , (5)
|
определяется аналогично эластичности спроса, но здесь Q - объем предложения, связанный с ценой функцией Q = S(P) (рис. 4). Так как объем предложения - неубывающая функция цены, эластичность предложения в обычных случаях - неотрицательная величина. В лекции 6 отмечался различный характер функции предложения в различных периодах. Это различие находит свое отражение в эластичности:
а) для мгновенного предложения, когда продукт уже произведен, его количество является величиной постоянной, Εp[S] = 0;
б) в коротком периоде предложение может в некоторой степени приспособиться к изменяющейся цене и на значительной части кривой предложения Εp[S] = 0; однако при этом возможности производства не безграничны, и по мере приближения к предельно возможному объему Q* (рис. 4) эластичность снижается, стремясь к нулю;
в) в длительном периоде возможности приспособления еще шире, а коэффициент эластичности больше, чем в среднем периоде. Ограниченность возможностей предложения при этом обычно не играет существенной роли.
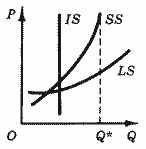
Рис. 4. Кривые предложения в различных периодах:мгновенном (IS), коротком (SS) и длительном (LS).
РАЗДЕЛ 2. Как измерить эластичность
В предыдущем разделе величина эластичности спроса по цене определялась для каждого значения цены, т. е. для каждой точки кривой спроса. Это - точечная эластичность. Но часто нужно знать эластичность на некотором участке кривой, соответствующем переходу от одного состояния к другому (от точки М1 к точке M2 на рис. 5). Здесь видна аналогия с простой задачей из механики: скорость тела (мгновенная) есть производная от пройденного пути по времени; в то же время часто представляет интерес скорость (средняя), соответствующая определенному участку пути или промежутку времени.
Например, если автомобиль за 2 часа прошел 100 км, то его средняя скорость равна 100/2 = 50 км/ч.
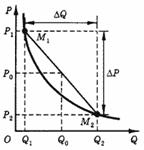
Рис. 5. К определению дуговой эластичности.
Интерес к интервальным характеристикам может быть связан с двумя обстоятельствами.
Во-первых, нас может интересовать участок кривой от текущего состояния до ожидаемого (планируемого, прогнозируемого). Во-вторых, определение точечной эластичности из предыдущего раздела использует операцию дифференцирования. Это обстоятельство не вызвало бы затруднения, если бы мы располагали аналитическим описанием функции спроса. Но наблюдение над реальным процессом не дает аналитического выражения, оно может дать лишь значения интересующих нас величин в отдельных точках.
Действуя по аналогии с механической задачей, мы могли бы определить эластичность спроса на участке кривой как частное от деления относительного изменения объема спроса на относительное изменение цены:
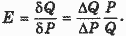 , (6) , (6)
|
Но аналогия с автомобилем оказывается неполной:
приращения ΔР = Р2 - Р1 и ΔQ = Q2 - Q1 и в нашем случае определяются начальным и конечным состояниями, но какие абсолютные уровни Р и Q следует использовать в формуле (6)? В принципе это могли бы быть и начальные (Р1, Q1), и конечные (Р2, Q2) значения. Оба варианта, очевидно, дадут различные результаты. В качестве компромиссных обычно выбирают средние значения обеих переменных:
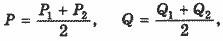 , ,
|
что в результате дает выражение эластичности:
 , (7) , (7)
|
Эластичность спроса, определяемая равенством (7), характеризует некоторую среднюю реакцию спроса на изменение цены на участке М1М2 и называется дуговой эластичностью.
Существует и другой подход к определению сред ней эластичности на участке кривой спроса, также аналогичный рассмотренной выше механической задаче, но в ином отношении. Средняя скорость - это скорость тела, движущегося равномерно (т. е. с постоянной скоростью) в течение того же времени, что и реальное тело, и проходящего за это время такой же путь. Подобно этому, мы можем рассмотреть кривую постоянной эластичности, проходящую через начальную и конечную точки рассматриваемой дуги, и в качестве характеристики дуги использовать эластичность этой кривой.
Функция с постоянной эластичностью - это степенная функция вида Q = APE (см. МП, II, формула (5)). У этой функции два параметра, и для ее однозначного определения достаточно располагать значениями переменных в двух точках:
 , ,
|
Почленно разделив второе из этих равенств на первое, получим:
 , (1) , (1)
|
откуда:
 , (8) , (8)
|
Выбор основания логарифмов здесь не играет роли. Формулы (7) и (8) дают не одинаковые, но довольно близкие результаты, даже если точки М1 и М2 не очень близки друг к другу.
Рассмотрим числовой пример:
Р1 = 10. Q1 = 50,
Р2 =5, Q2 = 70.
Используя формулу (7), получим:
 , ,
|
а формулу (8):
 , ,
|
Расхождение между этими результатами достаточно мало по сравнению с погрешностями, допустимыми в такого рода расчетах; обычные ошибки в исходных данных приводят к гораздо большим неточностям.
Второй из рассмотренных нами подходов может быть преобразован для случая, когда имеются не две, а большее число точек на кривой спроса. Пример таких данных приведен в табл. 3.
Таблица 3. Пять точек на кривой спроса
| Точка | Цена | Объем спроса |
Если число точек больше двух, мы не можем рассчитывать на то, что найдется кривая постоянной эластичности, проходящая через все эти точки. Вместо этого ищем кривую постоянной эластичности, ближайшую ко всей совокупности заданных точек.
Существуют вычислительные методы, позволяющие успешно решать такие задачи; мы их здесь рассматривать не будем. Укажем лишь метод, позволяющий приближенно решить такую задачу на глаз.
Для степенной функции Q = APE справедливо равенство:
log Q = а + E·log P,
где а = log A.
Иными словами, логарифмы Р и Q связаны линейной зависимостью. Поэтому, отложив по осям координат не сами наблюдавшиеся величины Р и Q, а их логарифмы, мы сведем задачу к нахождению прямой, наименее удаленной от заданных точек. А здесь уже возможны глазомерные прикидки. Угловой коэффициент этой прямой равен искомой эластичности. Такие построения удобнее всего выполнять на специальной логарифмической бумаге, разграфленной и отградуированной таким образом, что координаты точек пропорциональны логарифмам отмеченных на осях чисел. На рис. 6,б исходные данные представлены в логарифмических масштабах. Точки располагаются близко к некоторой прямой, что свидетельствует о том, что эластичность спроса во всем диапазоне представленных значений более или менее постоянна. В противном случае следовало бы разбить кривую на несколько участков и определять эластичность для каждого из участков в отдельности.
На рис. 6,а представлены те же данные в обычных (линейных) масштабах; там же нанесена ближайшая к ним кривая постоянной эластичности, рассчитанная точными методами. Ее уравнение Q = 747.8·P1.868, так что эластичность оценивается величиной Е = -1.868. То обстоятельство, что кривая не проходит точно через заданные точки, оказывается полезным: таким образом сглаживаются шероховатости, обусловленные погрешностями данных, и лучше выявляются закономерности изучаемого явления.
РАЗДЕЛ 3. Ценовая дискриминация
Часто бывает так, что продавец (монополист) ведет торговлю сразу на двух и более рынках, отделенных друг от друга.
На все эти рынки он поставляет одну и ту же продукцию, которую производит сам, но продается она по разным ценам: на каждом рынке он устанавливает свою цену. Такая продажа называется ценовой дискриминацией (англ. price discrimination). Термин "дискриминация" не заключает в себе никакого этического смысла. Он используется здесь с единственной целью - не путать обозначаемое им явление с дифференциацией цен в зависимости от качества товаров и услуг.

Рис. 6. Кривая постоянной эластичности. а - в обычных масштабах; б - в логарифмических.
Предположим теперь, что продукцию, продаваемую на сравнительно дешевом рынке, можно купить у монополиста, а затем перепродать на дорогом рынке. В этом случае цена на обеих (если их две) частях рынка окажется одинаковой. Она стала бы единой (одной) и в том случае, если бы постоянные покупатели дорогого рынка могли стать клиентами дешевого рынка. В обоих случаях ценовая дискриминация неосуществима.
Следовательно, для проведения ценовой дискриминации недостаточно простого разделения рынка на части. Для этого необходимо разделить его так, чтобы в той или иной степени было затруднено передвижение товаров между его частями. Только тогда части данного рынка могут стать отдельными, изолированными рынками, так что спрос на каждом из них не будет зависеть от цен, которые устанавливаются на другом рынке.
Самый типичный пример в данном случае - непосредственное предоставление частных услуг (врачами, адвокатами, учителями, владельцами гостиниц и т. п.). Так, врач, берущий с одних (состоятельных) пациентов более высокую плату, чем с других (неимущих), может не опасаться, что лица, оплачивающие его услуги ниже, перепродадут их тем, кто за такие же услуги платит больше.
О ценовой дискриминации можно говорить и тогда, когда рынки, на которых ведет торговлю монополист, отделены друг от друга географически или посредством тарифных барьеров. Как в том, так и в другом случае перемещение товаров со сравнительно дешевого рынка на тот, где их можно продать дороже, сопряжено со значительными расходами, что и служит препятствием для перепродажи (перемещения).
Единство рынка может быть нарушено и иначе. Нередки случаи, когда одинаковые по существу товары продаются под видом товаров разного качества.
Покупатели-снобы, приобретая дорогостоящие товары, выделяются среди покупателей относительно бедных. Тем самым рынок оказывается разделенным и монополист получает возможность проводить ценовую дискриминацию.
Обособление отдельных частей рынка обусловливает лишь формальную возможность для монополиста устанавливать разные цены на один и тот же товар. Но в чем же выгода ценовой дискриминации для монопольного производителя? В основе разных цен на данный единичный товар лежит разная эластичность спроса на тех изолированных рынках, где есть возможность продавать продукцию. И такая продажа выгодна монополисту.
В подтверждение этого рассмотрим рис. 7.

Рис. 7. Ценовая дискриминация.
Пусть монополист, проводящий ценовую дискриминацию, ведет торговлю на двух рынках - 1 и 2, которые характеризуются соответственно линиями спроса D1 и D2. Рынок 1 меньше по объему, но более эластичен. MR1 и МR2 - соответствующие линии предельной выручки.
Каким образом распределится общий объем предложения между рынками? Если, например, MR1 > МR2, то производителю выгодно часть товара перебросить с рынка 2 на рынок 1. При этом MR1 снизится, a МR2 возрастет. И только при MR1 = МR2 перераспределение товара между рынками не приведет к увеличению общей выручки. Это и будет наиболее выгодным распределением товара между рынками. Поэтому мы можем построить линию общей предельной выручки МRT, выполнив горизонтальное суммирование кривых MR1 и МR2, т. е. сложив объемы предложения при одинаковых значениях МR.
Пересечением МRT c МC - кривой предельных затрат - определяется общий объем выпуска продукции QT. Горизонтальная линия МRE, проходящая через точку пересечения Е, - это линия равной предельной выручки. Точки пересечения линии МRE с линиями предельной выручки MR1 и МR2 позволяют определить объемы продаж и цены для каждого рынка. На рынке 1 будет продано Q1 единиц товара по цене P1, а на рынке 2 - Q2 единиц товара по цене P2. Получаем: предельная выручка на каждом рынке одинакова и равна общей предельной выручке и предельным затратам на всю продукцию (MR1= МR2 = МRT = MC).
Предельный доход связан с эластичностью E спроса по цене соотношением:
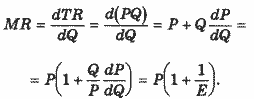 , ,
|
Поэтому равенство MR1 = МR2 можно представить в виде:
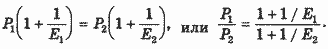 , ,
|
Если эластичность спроса будет одинакова (E1= E2), то равными будут и цены (P1= P2), т. е. ценовая дискриминация невозможна. При условии же, что эластичность спроса на разных рынках будет неодинакова, разными будут и цены. Если абсолютная величина эластичности спроса на рынке 1 будет больше, чем на рынке 2 (|E1|< |E2|), цена на рынке 1 будет меньше, чем цена на рынке 2 (P1< P2). Цена, которая установится на каждом из рынков, окажется ценой спроса на всю продаваемую там продукцию.
Итак, монополист может получить больше прибыли, если будет продавать меньше продукции на рынках, где эластичность спроса (и предельная выручка) ниже; на тех же рынках, где эластичность спроса (и соответственно предельная выручка) выше, он будет продавать больше продукции. Объем продаж установится тогда на уровне, при котором предельная выручка от реализации дополнительной единицы продукции будет равна на всех рынках. А если его предельная выручка от продажи продукции на каждом из рынков окажется равной его предельным затратам на производство всей продаваемой продукции, то монополист получит наибольшую прибыль.
Прибыльность монополии не в последнюю очередь зависит от того, каким способом тот или иной рынок разделен на части. Способов разделения рынка немало. Здесь же рассмотрим случай, когда монополисту предоставлена полная свобода действий.
Допустим, прежде всего, что в распоряжении монополиста есть некий ключ, с помощью которого он, по своему усмотрению, может отделить покупателей друг от друга.
Предположим также, что сначала он назначает на свой товар единую цену, а затем предпринимает усилия, направленные на последовательное разделение рынка на части.
Совокупный спрос на рынке складывается из спроса отдельных покупателей. При условии, что эластичность спроса этих покупателей одинакова, монополисту придется назначить единые цены по всему рынку; ценовая дискриминация не принесёт ему каких-либо выгод, а рынок останется неразделенным. Если же эластичность спроса отдельных покупателей неодинакова, то монополист поступит иначе. Он разделит их на две группы и сделает это так, что самая высокая эластичность спроса покупателей одной группы окажется ниже, чем самая низкая эластичность, характеризующая спрос покупателей второй группы.
Дальнейшие его шаги будут такими: на товары, которые приобретают покупатели первой группы, он повысит цену, а на товары для покупателей второй группы - понизит. После этого монополист вновь решает ту же задачу. Если теперь эластичность спроса всех покупателей, относящихся к той или иной группе, одинакова, то повторное разделение рынка утрачивает смысл. Но если она оказалась разной, то каждый из вновь образовавшихся рынков надлежит опять разделить (по тому же принципу) на два рынка. И это будет продолжаться до тех пор, пока на каждом рынке не останется группа покупателей (а в крайнем случае один-единственный покупатель) со спросом, характеризующимся одинаковой эластичностью. Наконец, остаются всего лишь два покупателя, спрос которых имеет неодинаковую эластичность, но приобретающие данную продукцию по одной и той же цене. И в этом крайнем случае монополист увеличит прибыль, если он продаст свою продукцию каждому из них по особой цене. Спору нет, монополист лишь в исключительных случаях может разделить рынок произвольно, руководствуясь лишь собственными устремлениями.
Всегда находятся всевозможные причины, препятствующие такому разделению рынка, которое для него являлось бы лучшим из всех возможных, т. е. обеспечивало бы наибольшую выгоду. И все же раздел рынка осуществляется, и стоит только этому произойти (в соответствии с эластичностью спроса на вновь возникающих рынках), как самая низкая цена назначается там, где эластичность спроса самая высокая, а самая высокая цена - где эластичность спроса самая низкая.
Задачи
1. В результате повышения цены товара с 5 до 6 р. объем спроса сократился с 9 млн шт. до 7 млн шт. в год. Общий уровень цен не изменился. Определите коэффициент прямой эластичности спроса по цене.
2. Дана функция спроса на товар X:
QDX = 8 - Px + 0,2Py
где Px и Py - цены товаров x и y. Допустим, Px = 4, Py= 5.
Определите коэффициенты прямой и перекрестной эластичности спроса по цене.
3. Дана функция спроса на некоторый товар:
QD = 8 - 0,6Р,
где Р - цена данного товара в рублях.
При какой цене коэффициент прямой эластичности спроса по цене равен -0.5?
4. Эластичность спроса населения на данный товар по цене равна -0.25. Эластичность спроса по доходу равна 0.8. На сколько процентов изменится объем спроса на данный товар, если его цена уменьшится на 8 %, а доходы населения увеличатся на 5%? При этом предполагается, что общий уровень цен останется неизменным.
5. Потребитель весь свой доход расходует только на три вида товаров: хлеб, колбасу и молоко. В настоящее время 20 % своего дохода он расходует на хлеб, 50 % - на колбасу и 30 % - на молоко. Определить эластичность спроса на молоко по доходу, если эластичность спроса на хлеб по доходу равна -1, а эластичность спроса на колбасу по доходу равна 2.
6. Эластичность спроса на продовольствие по доходу равна 0.8. Первоначально 50 % своих доходов население расходовало на продовольствие. Предположим, доходы населения увеличились на 10%. Определить долю расходов на продовольствие в доходах населения.
Лекция 8. Заменяемость и дополняемость
РАЗДЕЛ 0. У БАРБОСА ЕСТЬ ВОПРОСЫ. Товары заменяют или дополняют друг друга. Как это влияет на спрос?
ИГОРЬ. Так значит, мы уже знаем, что такое эластичность: с помощью коэффициента эластичности можно объяснить, что такое взаимозаменяемые и взаимодополняемые товары.
АНТОН. А разве это и так не ясно? Левый ботинок не может заменить правый, но нужны обязательно оба, чтобы можно было ими пользоваться. Это и есть дополняющие друг друга товары. Или другие примеры: корпус и стержень шариковой ручки, магнитофон и магнитная лента, автомобиль и бензин и т. д.
БАРБОС. Чрезвычайно важное свойство вещей! Ведь что бы я делал, если бы у меня была только мягкая подстилка, но не было бы миски с водой? Или, наоборот, была бы только миска с водой и не было бы подстилки?
ИГОРЬ. Я согласен с тобой, мы могли бы в нашем вводном уроке ограничиться такого рода объяснением. Достаточно ясно, например, что для любителя сладкого шоколад, конфеты, сахар, пирожные, варенье, сгущенка, мед - это все продукты взаимозаменяемые.
АНТОН. А что ты скажешь, например, о мандаринах, апельсинах, грейпфрутах? Или о возможности отдохнуть, читая книгу, лежа на диване, гуляя по лесу или парку?
ИГОРЬ. Все это верно, мне только хотелось бы спросить у тебя: что будет, если повысится цена на яблоки? Как ты отреагируешь на это, если тебе придется покупать, скажем, сливы, груши, виноград?
АНТОН. Ясно, что я куплю меньше яблок, но при этом куплю больше этих взаимозаменяемых товаров.
ИГОРЬ. Ну, а если повысятся цены на фотобумагу или фотопленку, то что произойдет со спросом на фотоаппараты?
АНТОН. Спрос снизится на то и на другое, потому что это взаимодополняемые товары.
ИГОРЬ. Теперь давай подумаем, каким будет коэффициент эластичности спроса на сливы, если цена на яблоки выросла на 10 %, а спрос на сливы повысился на 15 %?
АНТОН. Очень просто:15 разделить на 10 получается 1.5.
ИГОРЬ. Вот, вот, если коэффициент эластичности спроса на какой-то товар по цене другого товара больше нуля, то считается, что эти товары взаимозаменяемы. Такой коэффициент называется коэффициентом перекрестной эластичности.
АНТОН. Я заметил, что этот коэффициент рассчитывается с учетом знака числителя и знаменателя, а не только по абсолютной величине, как в прошлой лекции, где мы считали коэффициент спроса на яблоки при изменении цены на те же яблоки.
ИГОРЬ. Справедливое замечание. Именно поэтому, если цены на фотопленку повысятся на 10 %, а спрос на фотоаппараты упадет на 15%, то коэффициент перекрестной эластичности будет меньше нуля (-15:10= -1.5), а это и означает, что данные товары дополняют друг друга.
АНТОН. А если коэффициент перекрестной эластичности равен нулю, то как это можно истолковать?
ИГОРЬ. Думаю, это означает, что такие товары независимые, т. е. изменение цены одного не оказывает влияния на спрос другого товара.
БАРБОС. Так, так, представим себе, что цена на костную муку (порядочная дрянь) поднялась и мне стали покупать больше нормальных вкусных косточек. Впрочем, кости я получаю из супа хозяев, и это никак не зависит от цены костной муки. Нет, мне нельзя так много думать, собакам это вредно. Может быть, читатель подскажет мне ответ?
РАЗДЕЛ 1. Кривая безразличия и норма замены
Сейчас мы приступаем к более подробному рассмотрению фундаментальных для экономического знания представлений о заменяемости и дополняемости. Для этого читателю необходимо познакомиться с рядом новых понятий.
Как, вероятно, помнит читатель (лекция 2), взаимосвязь между спросом на товар и его ценой определяется полезностью товара с позиции потребителя. В лекции 2 полезность каждого товара рассматривалась изолированно - полезность зависела лишь от количества приобретаемых единиц данного товара. Очевидно, однако, что в реальной действительности спрос потребителя на некоторый товар зависит от намерений по закупке других товаров не только с точки зрения ограниченного бюджета (чем больше средств тратится на яблоки, тем меньше остается на книги), но и с точки зрения полезности (чем больше покупается яблок, тем меньше нужно груш). Иными словами, потребитель сталкивается с необходимостью выбора оптимального набора или комбинации нескольких (а в более широком смысле - всех) приобретаемых им товаров, причем сокращение потребления одного товара может быть заменено (компенсировано) увеличением потребления другого товара без снижения общей полезности данного товарного набора.
Проблема выбора оптимального набора товаров привела в экономической науке к возникновению техники, так называемых кривых безразличия, которая и будет проиллюстрирована в настоящем разделе на примере двух товаров.
Представим себе, что потребителю нужно выбрать некоторую комбинацию двух товаров.
Очевидно, любой акт выбора имеет две стороны: желания (которые определяются вкусами и предпочтениями) и возможности (доступность товаров для потребителя).
Для анализа потребительских предпочтений как раз и служат кривые безразличия.
Поясним это на примере. Пусть некто решает приобрести 10 яблок и 20 конфет.
Попробуем определить, какие другие наборы (комбинации) яблок и конфет имеют, с точки зрения потребителя, общую полезность, равную полезности этого первоначального набора. Иначе говоря, потребителю безразлично, какой из этих наборов выбрать (причем безразлично с точки зрения вкуса, а не цен). Представим полученные данные в табл. 1.
Таблица 1. Наборы яблок и конфет, имеющие для потребителя равную суммарную полезность
| Набор | Яблоки | Конфеты |
| А | ||
| В | ||
| С | ||
| D | ||
| Е | ||
| F |
Представим теперь информацию табл. 1 графически. Будем откладывать по вертикальной оси количество яблок, а по горизонтальной - количество конфет с тем, чтобы каждому наборуэтих двух товаров соответствовала бы точка в графическом "пространстве товаров".
Отметим теперь на графике точки, соответствующие наборам А-F из табл. 1.
На рис. 1 эти точки соединены плавной линией ii. Разумно предположить, что все точки, лежащие на этой линии, характеризуют комбинации товаров, имеющие для потребителя равную общую полезность (т. е. потребителю безразлично, какую из этих комбинаций выбрать). Поэтому линия ii называется кривой безразличия.
Рассмотрим любую комбинацию товаров, лежащую выше кривой ii (например, комбинацию К - 20 яблок и 20 конфет).
Доставит ли эта комбинация потребителю большее удовлетворение, чем комбинации, лежащие на кривой безразличия (например, комбинация А)? Рассмотрим количество яблок и конфет в обоих наборах:
Комбинация А Комбинация К
30 яблок 20 яблок
б конфет 20 конфет
Вопрос остался открытым, так как неизвестно, что в этом случае предпочтительнее для потребителя: 10 лишних яблок или 15 лишних конфет. Однако мы знаем другое: общая полезность набора А равняется общей полезности набора С (13 яблок и 15 конфет).
Сравним тогда комбинацию К с комбинацией С:
Комбинация С Комбинация К
13 яблок 20 яблок
15 конфет 20 конфет
Очевидно, что комбинация К будет иметь для потребителя полезность большую, чем полезность комбинации С, а следовательно, и комбинации А и всех других комбинаций, лежащих на кривой безразличия ii.
Из приведенных выше рассуждений можно с уверенностью заключить, что любая точка, лежащая выше кривой безразличия ii, будет более предпочтительной для потребителя, чем точки кривой безразличия. С другой стороны, любая точка, лежащая ниже кривой безразличия ii (например, точка Н на рис. 1), дает потребителю меньшее удовлетворение, чем точки кривой безразличия.
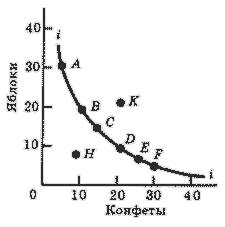
Рис. 1. Кривая безразличия.
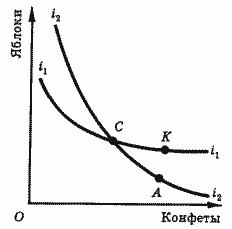
Рис. 2. Пересечение кривых безразличия: такого быть не может!
Сформулируем теперь некоторые общие свойства кривых безразличия.
1.Через любую точку в графическом пространстве товаров (рис. 1) может быть проведена соответствующая кривая безразличия, т. е. для любой комбинации товаров (яблок и конфет) могут быть найдены другие комбинации, имеющие для потребителя такую же общую полезность.
Это свойство основывается на простом предположении о том, что потребитель может сравнивать с помощью отношений предпочтения или безразличия все возможные наборы товаров.
2.Две кривые безразличия не могут пересекаться.
Рассмотрим рис. 2. Предположим, что кривые безразличия i1i1 и i2i2 пересекаются в точке С. Тогда потребитель безразличен в выборе между С и А и в выборе между С и А.
Следовательно, потребитель безразличен в выборе между К и А. Но точка А лежит ниже кривой i1i1, поэтому, как нам уже известно, полезность комбинации А меньше полезности комбинации К. Очевидно, что пересечение кривых безразличия невозможно.
3. На основании свойств 1 и 2 может быть построена карта безразличия потребителя (рис. 3).

Рис. 3. Карта безразличия.
Комбинации товаров, лежащие на более высоких кривых безразличия, имеют для потребителя большую полезность (по правилу о точках, лежащих выше кривой безразличия).
4. Кривые безразличия имеют отрицательный наклон, так как уменьшение количества одного товара должно быть заменено (компенсировано) увеличением количества другого товара для сохранения общей полезности набора товаров.
5. Свойства 1-4 достаточно наглядны и не вызовут, вероятно, возражений читателя.
Однако они не объясняют в полной мере используемой нами формы кривых безразличия.
Действительно, эти свойства характеризуют, например, кривые, изображенные на рис. 4.

Рис. 4. Кривые безразличия.
Применяемые же нами кривые безразличия (рис. 1-3) имеют вполне определенную форму - все они являются выпуклыми по отношению к началу координат (наклон кривых безразличия уменьшается при движении вправо вдоль горизонтальной оси). Попробуем объяснить, с чем связано такое предположение. Рассмотрим еще раз пример с конфетами и яблоками (табл. 1).
Легко заметить, что при переходе от набора А к набору В, от набора В к набору С и т. д. потребитель всякий раз получает пять дополнительных конфет, но количество яблок, которое он при этом теряет, все время уменьшается от 12 (при переходе от А к В) до одного (при переходе от Е к F). В этом случае говорят об уменьшающейся предельной норме замены. Предельной нормой замены одного товара другим (яблок конфетами) называется количество яблок, которое потребитель согласен потерять с тем, чтобы получить одну дополнительную конфету (при одинаковой общей полезности комбинаций товаров).
Предельная норма замены = -ΔY / ΔX.
Таблица 2. Уменьшение предельной нормы замены
| Переход | Изменение количества яблок(ΔY) | Изменение количества конфет(ΔX) | Предельная норма замены |
| От набора А к набору В | -12 | +5 | 12 / 5 = 2.4 |
| От набора В к набору С | -5 | +5 | 5 / 5 = 1 |
| От набора С к набору D | -3 | +5 | 3 / 5 = 0.6 |
| От набора Л к набору Е | -1 | +5 | 2 / 5 = 0.4 |
| От набора Е к набору F | -1 | +5 | 1 / 5 =0.2 |
Как видно из табл. 2, предельная норма замены на кривой безразличия ii (рис. 5) уменьшается от 2.4 до 0.2. Это уменьшение легко объяснить логически. В точке А потребитель имеет относительно много яблок и относительно мало конфет. При движении от точки А вправо по кривой безразличия количество яблок уменьшается, а количество конфет увеличивается. Очевидно, чем больше конфет уже имеется у потребителя, тем меньшим количеством все более дефицитных яблок он готов пожертвовать, чтобы получить дополнительную конфету.
На рис. 5 легко увидеть (и доказать), что предельная норма замены графически характеризуется наклоном кривой безразличия. Таким образом, предположение об уменьшающейся предельной норме замены привело нас к пятому свойству кривых безразличия: наклон кривой безразличия уменьшается при движении вправо, кривые безразличия выпуклы по отношению к началу координат.

Рис. 5. Уменьшающаяся предельная норма замены.
Рассмотрим теперь два особых случая конфигурации кривых безразличия. Отметим прежде всего, что многие товары находятся друг с другом в отношениях взаимозаменяемости и взаимодополняемости с точки зрения потребителей.
Взаимозаменяемыми называют товары, которые служат для удовлетворения одинаковых или сходных потребностей, так что потребитель может выбрать какой-то один из этих товаров (сигареты различных марок). С другой стороны, товары, которые потребляются совместно (спички и сигареты), называются взаимодополняемыми. Представим кривые безразличия для двух крайних случаев: совершенной взаимозаменяемости (если потребителю все равно, какие сигареты купить) и жесткой взаимодополняемости (если спички используются только при курении).
В случае совершенной взаимозаменяемости два товара рассматриваются как один товар, и кривая безразличия вырождается в прямую линию (рис. 6), т. е. предельная норма замены становится постоянной величиной.
При жесткой взаимодополняемости (рис. 7) каждому уровню удовлетворения потребителя соответствует одна комбинация товаров.
Увеличение количества одного товара без увеличения количества другого не изменяет полезности этой комбинации для потребителя (предельная норма замены равна нулю).
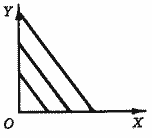
Рис. 6. Совершенная взаимозаменяемость.

Рис. 7. Жесткая взаимодополняемость.
Такие ситуации редки на практике. Большинство реальных кривых безразличия находятся между двумя крайними положениями, а многие товары являются взаимозаменяемыми и взаимодополняемыми в той или иной мере.
Так, все продукты питания в какой-то степени взаимозаменяемы, в то же время они могут быть взаимодополняемыми при приготовлении салатов, пирогов, подготовке праздничного ужина т. д. (и все это зависит от вкусов). Вообще поиск связей в отношении взаимодополняемости и взаимозаменяемости товаров - необыкновенно интересное и сложное занятие. Как связано между собой потребление пива и газет, билетов на концерт и садовых домиков, автомобилей и магнитофонных кассет? Пусть читатель сам ответит на эти вопросы или попробует придумать другие, более интересные цепочки товаров.
РАЗДЕЛ 2. Бюджетная линия и равновесие потребителей
В предыдущем разделе мы рассматривали одну сторону потребительского выбора - желания. Теперь остановимся вкратце на другой стороне - возможностях. Подобно тому как для анализа вкусов и предпочтений служат кривые безразличия, для анализа возможностей потребителей используются бюджетные линии (линии цен).
Предположим, потребитель имеет некоторую сумму денежных средств (М), которую он хотел бы израсходовать на приобретение товаров X и Y, цены на которые соответственно Px и PyПотребитель может поступить по-разному: израсходовать все свои средства на приобретение товара X или, наоборот, товара Y, а может выбрать какой-либо промежуточный вариант. Но в любом случае доступные потребителю комбинации товаров должны удовлетворять простому равенству:
| M = PyX + PyY, (1) |
где М - доход потребителя; X и Y - количество единиц товаров X и Y, приобретаемые потребителем;Px и Py- цены товаров X и Y.
Выражение (1) может быть записано в другом виде:
| PyY = М - PxX, |
или:
| Y = М/Py - Px/Py ·X. (2) |
В выражении (2) М /Py- постоянная величина, а -Px / Py- коэффициент при переменной X.
Таким образом, в выражении (2) прослеживается функциональная связь между количествами единиц товаров X и Y, приобретаемых покупателем. Графическим отображением этой связи в пространстве товаров является прямая линия с отрицательным наклоном (читатель без труда докажет это, вспомнив, что уравнение прямой Y = AX + В, и обратив внимание на знак "минус" в выражении (2)). Такая прямая называется бюджетной линией (рис. 8).

Рис. 8. Бюджетная линия.
Любая комбинация товаров, которая удовлетворяет выражениям (1) и (2), представлена точкой на бюджетной линии. Теперь мы можем провести совместный анализ желаний и возможностей потребителя, т. е. изобразить на одном графике его карту безразличия и бюджетную линию (рис. 9).
Потребитель, стремящийся максимизировать полезность приобретаемой комбинации товаров, остановится, безусловно, на комбинации Е - в точке пересечения бюджетной линии с наиболее высокой из пересекающих ее кривых безразличия i3. На рис. 9 видно, что в любой другой точке бюджетная линия АВ пересекается кривыми безразличия, лежащими ниже кривой i3, т. е. полезность соответствующих этим точкам комбинаций товаров меньше, чем полезность комбинации Е. Точка Е - точка оптимального потребительского выбора, или точка равновесия потребителя.
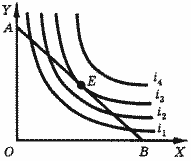
Рис. 9. Карта безразличия и бюджетная линия.
Очевидно, что в этой точке угол наклона кривой безразличия ΔY / ΔX равен углу наклона бюджетной линии -Px / Py, или, другими словами, норма замены равна обратному отношению цен. Норма замены показывает, в какой пропорции потребитель хочет заменить один товар другим, а соотношение цен говорит о том, в какой пропорции он может это сделать. Совпадение этих пропорций характеризует точку Е именно как точку равновесия потребителя: у потребителя отсутствуют мотивы замены равновесного набора товаров каким-либо другим.
Таким образом, здесь мы познакомились еще с одним понятием равновесия. Общая идея равновесия оказалась чрезвычайно плодотворной в теории рынка, и слово "равновесие" в различных сочетаниях будет еще не раз встречаться в наших лекциях.
РАЗДЕЛ 3. Понятие о частичном и общем равновесии
При анализе равновесия на рынке одного товара (лекция 1) положение равновесия определялось спросом и предложением данного товара, при этом совершенно не учитывалась ситуация на рынке других товаров.
Читатель, уже знакомый из предыдущего раздела с понятием о взаимозаменяемости и взаимодополняемости товаров, может задать вопрос: "А правомерен ли вообще был подобный подход?".
Ведь спрос на товар зависит не только от его цены, но и от цен всех заменяющих и дополняющих его товаров. Точно так же и предложение товара зависит от цен на все эти товары, а также на производственные ресурсы. Очевидно, что нарушение равновесия на рынке одного товара окажет влияние на множество других рынков, а это в свою очередь может вызвать ответное воздействие на рынок данного товара. Вопрос лишь в силе таких влияний.
Иногда они настолько малы, что ими можно пренебречь без серьезного ущерба для результатов анализа, иногда же учет их обязателен.
Существует два подхода к проблеме экономического равновесия. Один из них - с позиций частичного равновесия, когда рассматриваются один, два, три и т. д. рынка, взятых изолированно от остальной экономики. Другой - с позиций общего равновесия, когда рассматривается вся экономическая система в целом со всеми ее внутренними связями и взаимными влияниями. Выбор метода анализа в каждом случае зависит от цели исследования и конкретной рыночной ситуации.
Представим себе, что в силу каких-то причин выросла цена картофеля. С позиций частичного равновесия (т. е. при прочих равных условиях) спрос на него должен упасть, и зачастую это действительно так. Однако всегда ли? Ведь если цены других продуктов питания вырастут еще больше, чем цена картофеля, спрос на него может даже возрасти.
Но ведь и производители могут в этом случае использовать свою землю не для выращивания картофеля, а для других, ставших относительно более выгодными продуктов.
Вместе с тем рост дохода
|
|
|
|
Дата добавления: 2014-01-13; Просмотров: 1443; Нарушение авторских прав?; Мы поможем в написании вашей работы!