Свойства координат векторов

1. Координаты нулевого вектора в любом из базисов равны нулю.

2. Координаты вектора в данном базисе определяются однозначно.

3. При сложении векторов их соответствующие координаты складываются.

4. При умножении вектора на число все его координаты умножаются на это число.

5. Координаты линейной комбинации векторов равны таким же линейным комбинациям соответствующих координат слагаемых.

Эти свойства кажутся вам естественными, а докажем мы их позже.

Из 4-го свойства на основании теоремы 1 § 1 получаем еще один критерий коллинеарности: для коллинеарности векторов 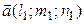и необходимо и достаточно, чтобы их координаты были пропорциональными, т.е., чтобы существовало число такое, что . Если все координаты ненулевые, то условие их пропорциональности можно записать и так: .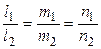

Системой координат называется совокупность точки О, которая называется началом координат, и базиса.

Если в пространстве задана система координат , то каждой точке можно поставить в соответствие вектор , который называется радиус-вектором этой точки.

Координатами точки в выбранной системе координат называются координаты её радиус-вектора в соответствующем базисе.

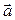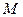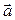Пусть при откладывании некоторого вектора от точки получается точка (рис. 1.15). Тогда вектор обозначается , а операция откладывания вектора от точки записывается следующим равенством:

. (6)

Так как

(7)

и т.к. координаты точки совпадают с координатами ее радиус-вектора, то из (6) и (7) получается правило: чтобы найти координаты конца вектора следует к координатам вектора прибавить соответствующие координаты его начала. Равенство (7) также равносильно равенству , из которого получаем: чтобы найти координаты вектора, следует из координат его конца вычесть соответствующие координаты начала.

Введенная система координат называется аффинной. Если базисные векторы попарно ортогональны, а длины их равны единице, то базис называется ортонормированным, а система координат – прямоугольной декартовой.

Дата добавления: 2014-01-13