Свойства смешанного произведения

Смешанное произведение

Определение. Смешанным произведением векторов , взятых в указанном порядке, называется число .

1 .Критерий компланарности. Для того чтобы три вектора были компланарными, необходимо и достаточно, чтобы их смешанное произведение равнялось нулю.

► Необходимость. Дано: 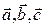–компланарны. Тогда

{существует плоскость P, что .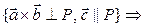

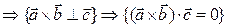Достаточность. Дано: . Рассмотрим два случая:

а);

б)

плоскость

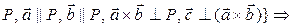
плоскость .◄

2. Геометрический смысл смешанного произведения. Смешанное произведение некомпланарных векторов численно равно объёму V параллелепипеда, построенного на этих векторах, отложенных от одной точки, взятому со знаком плюс, если тройка векторов правая и минус, если левая.

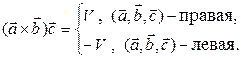(1)

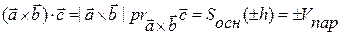►(см. рис. 1.23). Заметим, что на этом рисунке тройка – левая◄

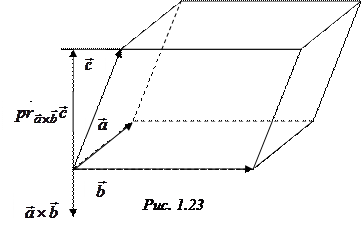3. .

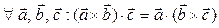►На основании коммутативности скалярного произведения, достаточно доказать равенство . Если векторы 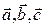компланарны, то утверждение истинно согласно первому свойству. Если же они некомпланарны, то

(2)

Так как ориентации троек и совпадают, то из (1) и (2) вытекает доказываемое утверждение. ◄

На основании этого свойства мы делаем вывод, что не имеет значения, в каком месте ставить «крестик», а в каком «точку». Поэтому в смешанном произведении эти знаки не ставятся вообще, и оно обозначается так: .

4. : .

►Первые три смешанных произведения равны вследствие того, что тройки одинаково ориентированы, а в последней тройке ориентация меняется, поэтому смешанное произведение меняет знак. ◄

5. : , , .

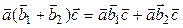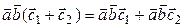►Докажем, к примеру, второе равенство:

.◄

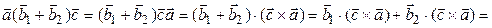
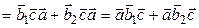6. .

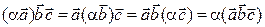Доказывается так же, как и предыдущее.

Дата добавления: 2014-01-13