Питання та задачі до самостійної роботи. 14.1 Основні поняття та визначення

Джерела інформації

МЕТОДИ ОПТИМІЗАЦІЇ БАГАТОВИМІРНИХ ЗАДАЧ

Лекція № 14

14.1 Основні поняття та визначення

14.2 Критерії оптимальності

14.3 Градієнтні методи

14.3.1 Найшвидший підйом з використанням одномірного пошуку

14.3.2 Метод найшвидшого спуску

14.3.3 Метод Флетчера – Рівса

14.3.4 Метод Девідона – Флетчера – Пауела

14.3.5 Метод конфігурацій Хука – Дживса

14.3.6 Метод конфігурацій Розенброка

1. Щуп Т. Решение инженерных задач на ЭВМ. – М.: Мир, 1982. – 235с.

2. Бахвалов Н. С. Численные методы. Т. И. Анализ, алгебра, обычные диференциальные уравнения. – М.: Наука, 1975. – 631 с.

3. Ляшенко М.Я., Головань М.С. Чисельні методи: Підручник. Либідь. 1996. – 288 с.

3. Крылов В. И. и др. Численные методы. – М.: Наука, 1978. – 1979. – Т. 2. – 400 с.

4. Форсайт Дж., Малькольм., Моулер Р. Машинные методы математических вычислений. – М.: Мир, 1980. – 279c.

5. Д. Мэтьюз, Г. Цинк, Д. Куртис. Численне методы. Использование Matlab, –М. Издательский дом “Вильямс”, 2001. – 720 с. 720 с.

6. Гил Ф., Мюрей У. Численные методы условной оптимизации. – М.: Мир, 1977. – 290 с.

7. Василев Ф. П. Лекции по методам решения експериментальных задач. – М.: Изд – во Моск. Ун – то, 1984. – 374 с.

8. Полак Е. Численные методы оптимизации. – М.: Мир, 1974.

9. Пшеничний Б. Н., Данилин Ю. М. Численные методы в екстремальных задачах. – М.: Наука, 1975.

10. Моделирование и оптимизация на ЭВМ радиоэлектронных устройств / Под ред. З. М. Бенесона. – М.: Радио и связь, 1981. – 272 с.

11. И.В. Кузьмин, М.М. Биков, С.М. Москвина, А.И. Кузьмин. Методы оптимизации сложных систем. – Винница: ВДТУ, 2003. – 165с.

1. Що таке градієнт і антиградієнт? Поясніть математично.

2. В чому полягає сутність градієнтних методів пошуку оптимуму цільової функції.

3. Поясніть узагальнену математичну модель градієнтних методів пошуку оптимуму функції.

4. Покажіть, що функція 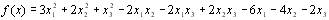є випуклою.

5. Знайдіть і класифікуйте стаціонарні точки функції .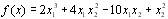

6. Проведіть аналіз визначеності наступних квадратних форм:

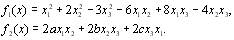
Дата добавления: 2014-01-13