Питання та задачі до самостійної роботи. 1. В чому полягає властивість унімодальності функцій і в чому полягає важність цієї властивості при розв’язку задач оптимізації з однією змінною?

1. В чому полягає властивість унімодальності функцій і в чому полягає важність цієї властивості при розв’язку задач оптимізації з однією змінною?

2. Якщо точка цільової функції задовольняє достатнім умовам існування локального мінімума, то як встановити чи є цей мінімум глобальним?

3. Чи є методи виключення інтервалів в цілому більш ефективними, ніж методи точкового оцінювання? Чому?

4. При реалізації пошукових алгоритмів на ЕОМ в якості умови закінчення ітераційного процесу використовуються як аналіз абсолютної величини різниці поточних значень кінців відрізка дослідження, так і абсолютної величини різниці поточних значень цільової функції. Чи можлива ситуація, коли результат однієї з перевірок вказує на збіжність до точки мінімума, тоді як отримана точка в дійсності мінімуму не відповідає. Поясніть відповідь рисунком.

5. Задані наступні функції однієї змінної:

а) ;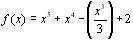

б) .

Для кожної з заданих функцій знайдіть:

· інтервал(и) зростання, спадання;

· точки перегину (якщо такі існують);

· інтервал(и), в якому функція вогнута, випукла;

· локальний і глобальний максимуми (якщо такі існують);

· локальний і глобальний мінімуми (якщо такі існують).

6. Встановіть області, в яких наступна функція випукла чи вогнута: . Знайдіть глобальний максимум і глобальний мінімум цієї функції.

7. В чому суть алгоритму методу дихотомії? Складіть схему алгоритма цього методу. Виберіть і обґрунтуйте умову виходу з ітераційного циклу.

8. Дослідіть функцію в інтервалі -44. Знайдіть локальні мінімуми, локальні максимуми, глобальний мінімум і глобальний максимум f в заданому інтервалі.

9. В чому сутність алгоритму методу Фібоначчі? Складіть схему алгоритма методу, наведіть основну математичну модель методу.

10. Розробіть програму для ЕОМ, яка реалізує пошук оптимуму за методом золотого перетину і методом Фібоначчі для функції 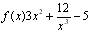в інтервалі 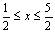. Порівняйте результуючі інтервали пошуку, які отримані за допомогою перерахованих методів.

Дата добавления: 2014-01-13