Частотная форма представления

Временная форма представления.

Характерные примеры математических моделей элементарных детерминированных сигналов.

1.функция Дирака

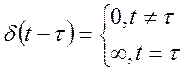
Свойства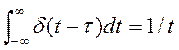

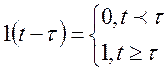
f(t)

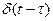
t t

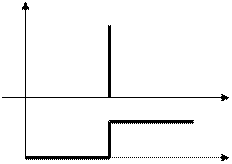
1(t-t)

t

2. Гармоническое колебание

X(t)=acos(ωt+j)

периодическая функция с периодам Т,а - амплитуда, ω=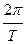, φ-началная фаза.

Основой для описания матической модели произвольных детерминированных сигналов спектральное представление функции в виде ряда или интеграла Фурье.

Известно что всякая периодическая фунция f(x) удовлетворяется на отрезке [O,T] условиям Дирихле (кусочно-дифференциальная функция, конечное число точек разрыва, конечное число экстремумов)

Может быть разложена в ряд Фурье (представлена точно или приближенно суммой гармоник с соответствующим постоянным коэффициентом):

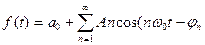
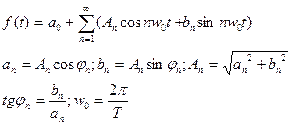
Комплексная форма

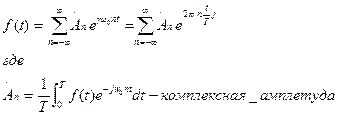
Таким образом, если f(t) имеет конечную длительность (т.е. ограничение во времени), она может как угодно точно представлена суммой элементарных детерминированных сигналов типа синусоиды. При этом каждый сигнал характеризуется своей амплитудой 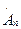и начальной фазой n-ой гармоники основной частоты 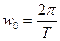функции f(t).

Спектр такой функции линейчатый пусть 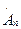=0,6+j0,3 таким образом:

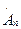=υ(0,6)²+(0,3)²=0,67

φ_ņ=αrctg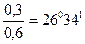

А(ω)

А₃

А₂ А_n-1

А₁ А_n

Реальная система, имеет конечную полосу пропускания, поэтому пропускает не все частоты. Сигнал определяется конечным числом ряда

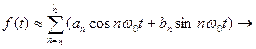
число членов ряда m=2TF,

где 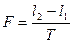- полоса частот занимаемой сигналом.

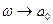-постояннаясоставляющая, физический смысл – среднее значение сигнала за период

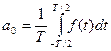
Обобщение на случай не периодичного сигнала непериодическая функция – предельный случай периодической функции с неограниченно возрастающим периодом.

Пр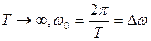и и 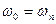- принимает любое значение 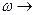, обозначим:

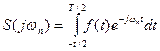(1)

и подставим в (2), учитывая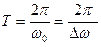

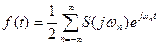(2)

Путем представления перехода при 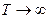получим:

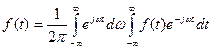
или порой преобразования Фурье:

прямое:

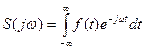
обратное:

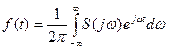
Таким образом, f(t) (непериодический сигнал) представляется в виде суммы бесконечно большого числа гармоник с непрерывной меняющейся частотой 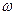и бесконечно малыми комплексными амплитудами колебаний.

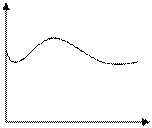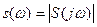
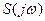= комплексная функция частот выражает спектральную плотность сигнала и называется спектральной или комплексным спектром. Модуль 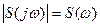- спектр сигнала. Структура спектра непериодического сигнала полностью определяется следующими функциями частот:

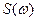- спектр амплитуд

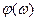- спектр фаз

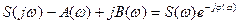
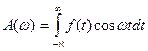
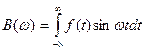
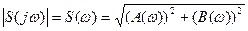
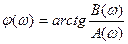
Дата добавления: 2014-01-13