Центральные проекции

Центральные проекции любой совокупности параллельных прямых, которые не параллельны проекционной плоскости, будут сходиться в точке схода. Параллельные прямые в трехмерном пространстве пересекаются лишь в бесконечности, поэтому точку схода можно представить себе как проекцию точки, находящейся в бесконечности. Существует бесконечное число точек схода.

Если совокупность прямых параллельна одной из главных координатных осей, то их точка схода называется главной точкой схода. Имеются только три такие точки, соответствующие пересечениям главных координатных осей с проекционной плоскостью. Например, если проекционная плоскость пересекает одну только ось z (и, следовательно, перпендикулярна ей), то лишь на этой оси будет лежать главная точка схода, поскольку прямые, параллельные как y-, так и x-осям, параллельны также и проекционной плоскости и поэтому не имеют точки схода.

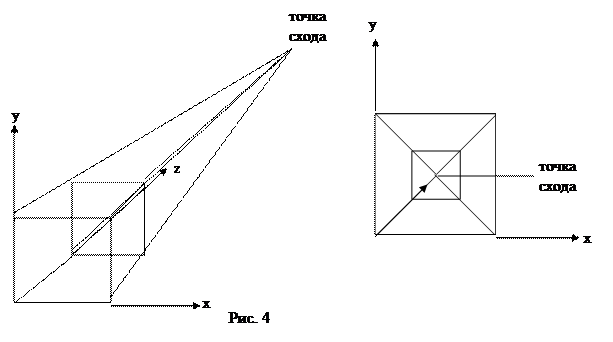Центральные проекции классифицируются в зависимости от числа главных точек схода, которыми обладают, а следовательно и от числа координатных осей, которые пересекает проекционная плоскость. На рис. 4 приведены две различные одноточечные проекции

куба. Ясно, что это – одноточечные проекции, поскольку прямые параллельные осям x и y, не сходятся, а сходятся только линии, параллельные оси z

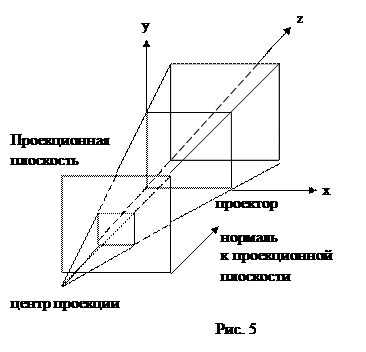
На рис. 5 показан процесс построения одноточечной, центральной проекции, некоторые из ее проекторов, а также проекционная плоскость, пересекающая одну лишь ось z.

Параллельные проекции.

Параллельные проекции разделяются на два типа в зависимости от соотношения между направлением проецирования и нормалью к проекционной плоскости. В ортографических параллельных проекциях эти направления совпадают, а в косоугольных параллельных проекциях они не совпадают. То есть в ортографических проекциях направление проецирования является нормалью к проекционной плоскости.

Наиболее широко используемыми видами ортографических проекций являются вид спереди, вид сверху (план) и вид сбоку, в которых картинная плоскость перпендикулярна главным координатным осям, совпадающим вследствие этого с направлением проецирования.

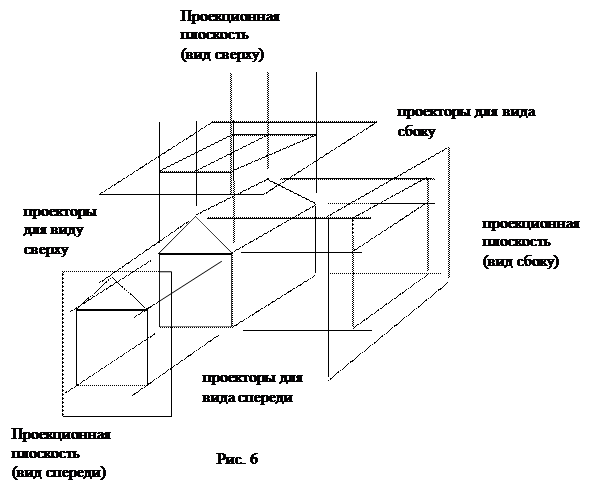
На рис. 6 показан процесс построения каждой из этих трех проекций, которые часто применяются в инженерной графике для описания машиностроительных деталей, агрегатов и сооружений, так как по ним можно измерять расстояния и углы. Поскольку каждая проекция отображает лишь одну сторону объекта, часто совсем не просто представить себе пространственную структуру проецируемого объекта, даже если рассматривать сразу несколько проекций одного и того же объекта.

В случае аксонометрических ортографических проекций используются проекционные плоскости, не перпендикулярные главным координатным осям, поэтому на них изображаются сразу несколько сторон объекта, так же как и при центральном проецировании, однако в аксонометрии укорачивание постоянно, тогда как в случае центральной проекции оно связано с расстоянием от центра проекции. При аксонометрическом проецировании сохраняется параллельность прямых, а углы изменяются; расстояния же можно измерить вдоль каждой из главных координатных осей (в общем случае с различными масштабными коэффициентами).

Широко используемым видом аксонометрической проекции является изометрическая проекция. В этом случае нормаль к проекционной плоскости (следовательно, направление проецирования) составляет равные углы с каждой из главных координатных осей. Если нормаль к проекционной плоскости имеет координаты (a, b, c), то потребуем, чтобы |a|=|b|=|c|. Имеются ровно восемь направлений (по одному в каждом из октантов), которые удовлетворяют этому условию, однако существуют лишь четыре различные изометрические проекции (если не рассматривать удаление скрытых линий), поскольку векторы (а, а, а) и (–а, –а, –а) определяют нормали к одной плоскости. Единичными нормалями этих направлений являются векторы (а, а, а), (–а, а, а) и (а, –а, а).

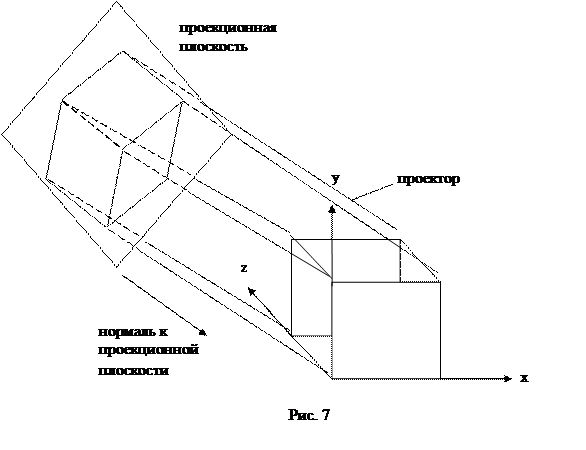
На рис. 7 показан процесс проекции с направлением (1, –1, 1).

Изометрическая проекция обладает следующим свойством: все три главные координатные оси одинаково укорачиваются. Поэтому можно проводить измерения вдоль направления осей с одним и тем же масштабом (отсюда название: изо, что означает «равно», и метрия – «измерение»). Кроме того, главные координатные оси проецируются так, что их проекции составляют равные углы друг с другом.

Дата добавления: 2014-01-13