Представление пространственных форм

До сих пор рассматривалась возможность построения 3-х мерных линейчатых объектов на основе примитивов в виде отрезков. Однако возникают ситуации (особенно автоматизированное программирование), когда необходим вывод 3-х мерных форм:

-описание заданной формы (пластилиновой);

-процесс творческого создания формы объекта;

Представление пространственной формы с помощью набора из 12 отрезков (неоднозначность пространственного отображения формы)

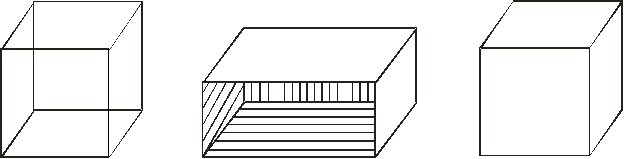
В общем случае, пространственную форму можно создать из примитивов более высокого уровня (чем 2-х мерная графика) => плоскости сферы и т.п.

При автоматизированном проектировании возникает проблема максимальноточного отображения формы (определение объемов, сечений, стирание скрытых областей), т.е. возникаетпроблемагеометрическогомоделированияобъектов.

Используются два способа изображения поверхностей в пространстве:

-полигональные сетки

-параметрические бикубические сплайны

1. Полигональные сетки.

П.С. – это совокупность связанных многоугольников.

Пример:

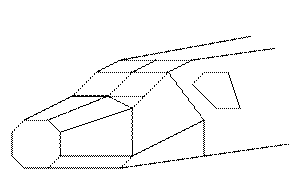
Недостаток: приблизительность моделирования объекта. При более детальной прорисовке необходимы большие вычислительные и временные затраты ЭВМ.

Для сложных объектов:

«+»простота алгоритмизации

«–»большой объем памяти

2. Параметрические бикубические поверхности.

Координаты точек искривленных поверхностей описываются с помощью 3-х уравнений (для x, y и z)

х=х;

y=f(x);

z=g(x);

Каждое уравнение имеет две переменные (би), показатель степени не выше 3-ей (куб). Границы поверхностей – это параметрические кубические кривые.

Пример:

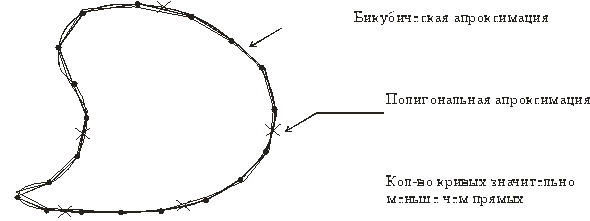
Преимущество: значительное снижение кусков аппроксимации, однако более сложная алгоритмизация.

«+»малый объем памяти

«-»время вычисления сплайнов

Методы описания полигональных сеток.

1. Явное задание многоугольников.

Многоугольник Р описывается:

P((x1,y1,z1),…(xn,yn,zn))

P – список координат вершин в порядке обхода многоугольника.

Недостаток:

-двойная прорисовка ребер

-для поиска многоугольников с одной вершиной необходимо сравнение пар ребер всех

примыкающих

-неоднозначность определения вершин при сравнении координат (потеря точности)

2. Указатели в список вершин.

Узел сетки запоминается лишь один раз в списке вершин:

V=((x1,y1,z1)…(xn,yn,zn))

Многоугольник определяется ссылкой на элемент списка.

Пример:

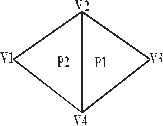
Список вершин:

V=(V1,V2,V3,V4) =((x1,y1,z1)…(xn,yn,zn))

Описание многоугольников:

P1=(1,2,4); P2=(4,2,3)

Преимущество: экономия памяти за счет однократного описания каждой вершины. Кроме того координаты вершин легко меняются.

Недостаток: трудно искать многоугольники с одинаковыми ребрами.

3. Явное задание ребер.

Имеется список вершин V. Имеется список Е, каждый элемент которого описан тетраэдр?!:

Е=(V1,V2, P1,P2)

V1 – вершина 1

V2 – вершина 2

P1 – многоугольник 1

P2 – многоугольник 2

Если ребро принадлежит одному многоугольнику, то одна из ссылок а – пуста.

Многоугольник определяется как ссылка на ребре Р=(Е1,...Еn)

Пример:

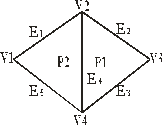
V=(V1,V2,V3,V4)=(x1,y1,z1,...)

E1=(V1,V2,P1, l)

E2=(V2,V3,P2, l)

E3=(V3,V4,P2, l)

E4=(V4,V2,P1,P2)

E5=(V4,V1,P1, l)

P1=(E1,E4,E5)

P2=(E1,E3,E4) E4 – не прорисовывается т.к. ссылка на P1

l = пусто

Вычеркиваются все ребра.

Для определения произвольной точки внутри многоугольника на плоскости можно пользоваться системой уравнений:

Ax+By+Cz+D=0 – уравнение плоскости

Ax1+By1+Cz1+D=0

Ax2+By2+Cz2+D=0

Ax3+By3+Cz3+D=0

Уравнения решаются относительно x,y,z.

Где: коэффициенты A,B,C,D определяются для плоскости по трем вершинам.

Дата добавления: 2014-01-13