Алгоритм плавающего горизонта

Работает в пространстве изображения. Используется для удаления невидимых линий трехмерного представления функций. Описывает поверхность в виде: F(x, y, z)=0

Главная идея – сведение 3-х мерной задачи к 2-х мерной, путем пересечения поверхности с постоянными координатами (плоскость z_i, постоянная координатная плоскость x, y).

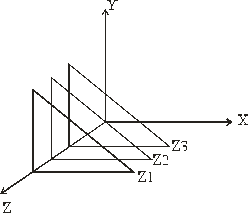
Затем все правые проецируются на плоскость z=0

y

x

z₁ z₂ z₃ z₄ z₅

x_i

y_i

z

y

x

z₁

z₂

z₃

z₄  

z₅

z₆

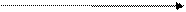
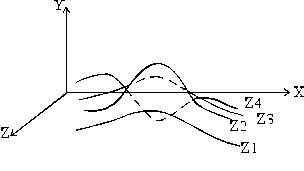
Алгоритм состоит в следующем

Начиная с ближней плоскости y=1 n,z=1 n

Проверка:

Если в точке xi значение yi больше значения всех предыдущих yij,

то точка видима;

Иначе точка yij не видима;

Ощущения «всплывания» горизонта при движении от z=1 до zn (или понижение невидимых точек)

При этом возможна ситуация «обратной» выпуклости

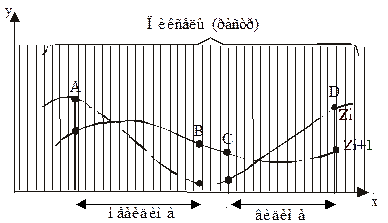
Поэтому требуется модернизация алгоритма (для плоскостей z1 до zn):

Если на текущей плоскости xi, yi > yijmax(пред.) или yi < yijmin(пред.)

то точка видна

Иначе не видна

Однако и этот алгоритм не совсем эффективен. Предположим следующую ситуацию:

Координата вычисляется в точках ABCD. Разложение в растр делает разрывы, т.к. в т. А уже принято решение о невидимости до т. В., в то же время в т. С принято решение о видимости до т. D. Таким образом, необходимо искать точки пересечения.

В данном случае можно воспользоваться линейной интерполяцией – точка пересечения двух прямых.

Либо методом половинного сечения. Возможно также появление линий последних плоскостей, выходящих за границы xmin и xmax, определяемые начальными плоскостями.

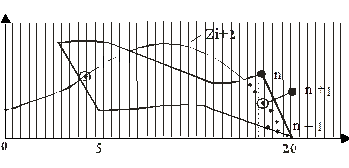
Это приводит к зазубренности линий ограничений.

Алгоритм Варнона

Работает в пространстве изображения.

Идея алгоритма: разбиение рабочей поверхности на ряд подэкранов.

Пример:

		удаление

При разрешении 256 256 пикселов требуется не более 8 шагов разбиения, чтобы достичь пиксела. Пикселы анализируются для каждой фигуры, и выбирается цвет ближайшего.

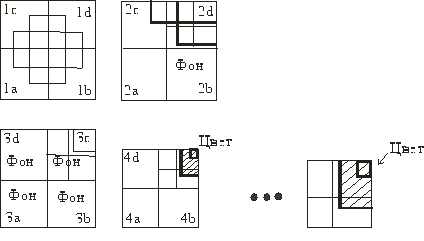
Возможны две ситуации:

1. разрешение по ребрам

1. 1. принимается на границе
   2. анализируется окружение если крайний, то отбрасывается т.к. многоугольник задан ребрами.
   разрешение по многоугольникам

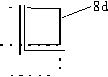
Для алгоритма управления линий 8d – пусто, значит фон.

Для удаления поверхностей необходима проверка соседних пикселов.

Если 8d соответствует многоугольнику, то окрашивается в цвет ближайшего к наблюдателю многоугольника, перекрывающему этот пиксел.

Реализация алгоритма осуществляется с помощью построения деревьев:

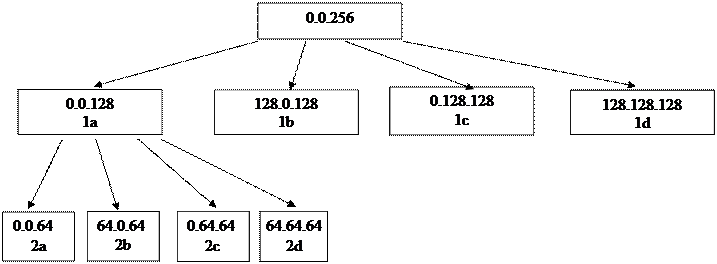
Алгоритм можно значительно упростить, если принять следующую систему приоритетов.

Рассмотрим случай, когда в окне находится 1 многоугольник.

Дата добавления: 2014-01-13