Полный сумматор

Если одноразрядный сумма­тор реализует сложение трех одноразрядных чисел А_i, B_i и C_i (перенос из младшего разряда), то такой сумматор называют полным.

Процедуру сложения двух n-разрядных двоичных чисел можно представить следующим образом: сложение цифр А₁ и В₁ младшего разряда дает бит суммы S₁ и бит переноса Р₁. В следующем (втором) разряде происходит сложение цифр Р₁, А₂ и В₂, которые формируют сумму S₂ и перенос Р₂. Операция длится, пока не будет сложена каждая пара цифр во всех разрядах.

В многоразрядном сумматоре только самый младший разряд можно выполнить по схеме полусумматора, а остальные разряды выполняют функции полного сумматора. Ниже рассмотрены схемы сумматоров для двоично-кодированных чисел.

Условное обозначение и условно графическое обозначение сумматора приведено на рис. 5.14.

Рис.5.14

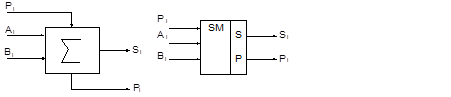Работа полного сумматора опи­сывается в таблице 5.9.

Таблица 5.9

Ai Bi Pi – 1	0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 0 0 0 0 1 1 1 1
Si Pi	0 1 1 0 1 0 0 1 0 0 0 1 0 1 1 1

Карта Карно для функций S_i и Р_i дает минимальную форму и ее тождествен­ные варианты:

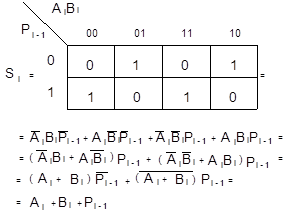
Соответственно выражениям на рис. 5.15 приведены различные реализации полного сумматора и его условное графическое изображение. Схема сумматора аналогична схеме на рис. 5.15, бпо структуре и парамет­рам, ее можно построить на основе двух полусумматоров (см. рис. 5.12,б). Сумматор по схеме на рис. 5.15,а, обладающий минимальной задержкой распространения сигнала и, следовательно, максимальным быстродействием, может с успехом применяться при построении БИС многоразрядного сумматора. Варианты полного сумматора на элементах И-ИЛИ-НЕ, реализуемый на ИМС промышленных серий, показан на рис. 5.15,г.

Рис. 5.15

Операция вычитания подобна операции сложения. Таблица истинности для операции вычитания приведа в таблице 5.10.

Таблица 5.10

Уменьшаемое Аi Вычитаемое Вi Заём из I – 1 Vi – 1	0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 0 0 0 0 1 1 1 1
Разность Di Заём из iVi	0 1 1 0 1 0 0 1 0 1 0 0 1 1 0 1

Дата добавления: 2014-01-13