Дифференциальные уравнения, описывающие процессы в цепях с сосредоточенными параметрами

Законы электрических цепей.

При анализе и расчёте электрических цепей используются два закона Кирхгофа. Рассмотрим их в применении к цепи с сосредоточенными параметрами.

2.1 Первый закон Кирхгофа применяется к узлам электрической цепи. Он вытекает из принципа непрерывности электрического тока. Охватим узел цепи замкнутой поверхностью S (рис.2.1).

Рис.2.1.

В соответствии с принятыми допущениями вся электрическая ёмкость в цепи с сосредоточенными параметрами предполагается сосредоточенной в конденсаторах, включённых в цепь. Это соответствует пренебрежению токами электрического смещения, отходящими от соединительных проводов к другим участкам цепи. Таким образом, через замкнутую поверхность S проходят только токи проводимости в проводниках, пересекающих эту поверхность. Согласно принципу непрерывности тока в данном случае получим:

, т. е.
- сумма токов, расходящихся от узла электрической цепи, равна нулю.
-плотность тока,

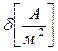
При любом числе ветвей имеем: 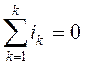, т.е. алгебраическая сумма токов, расходящихся от узла электрической цепи, равна нулю.

При составлении уравнений согласно первому закону Кирхгофа необходимо задаться условными положительными направлениями токов во всех ветвях, обозначив их на схеме стрелками. От узла, как правило, принимаем за положительное направление для токов, а знак «минус» приписываем токам, которые входят в узел. Для случая на рис.2.2 уравнение по первому закону Кирхгофа будет иметь вид:: - i₁ + i₂ + i₃ = 0

Рис.2.2.

Если в результате расчёта будет получено для некоторого тока в некоторый момент времени положительное число (i_k > 0), то это значит, что ток имеет в данный момент времени действительное направление согласно стрелок. Если же будет получено i_k < 0, то этот ток в действительности направлен против стрелки.

Второй закон Кирхгофа применяется к контурам электрической цепи. Он вытекает из соотношения:

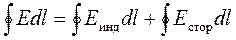
ЭДС, действующая вдоль некоторого пути, равна линейному интегралу вдоль этого пути напряжённости стороннего электрического поля, а также электрического поля, индуктированного изменяющимся магнитным полем.

Электрическое напряжение или падение напряжения связано с результирующим электрическим полем.

Электрическое напряжение вдоль некоторого пути от (·) А до (·) В равно линейному интегралу напряжённости результирующего электрического поля (электростатического, стороннего, индуктированного) вдоль этого пути.

Величина 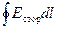равна сумме ЭДС.

источников сторонних ЭДС, действующих в контуре.

Величина 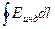включает в себя все индуктированные в контуре ЭДС, т.е. как ЭДС генераторов, действующих на принципе электромагнитной индукции, так и ЭДС взаимной индукции и самоиндукции, индуктируемых в катушках, включённых в контур. Обозначив сумму ЭДС источников энергии, действующих во всех параллельных ветвях контура в виде:

Будем иметь:

Итак, второй закон Кирхгофа гласит: алгебраическая сумма падений напряжений во всех ветвях любого замкнутого контура электрической цепи равна сумме ЭДС источников электрической энергии, действующих в этом контуре.

Если в k -той ветви содержится в общем случае участок с активным сопротивлением R_k, катушка индуктивности L_k и конденсатор с ёмкостью C_k, то падение напряжения вдоль всей этой ветви будет складываться из падений напряжений U_RK, U_CK, U_LK на этих элементах, т.е.

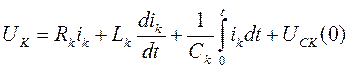
При составлении уравнений по второму закону Кирхгофа должны быть заданы положительные направления токов i_k иЭДС e_k источников энергии во всех ветвях. Положительные направления падений напряжений u_k считаем совпадающими с положительными направлениями токов i_k

2.3 Энергетические расчёты в цепях постоянного тока

При выполнении энергетических расчётов в цепях постоянного тока определяют следующие характеристики, связанные с распределением электрической энергии по элементам цепи:

- определение мощности, рассеиваемой в сопротивлениях цепи;

- определение суммарной рассеиваемой мощности;

- определение мощности, которую отдаёт в цепь источник напряжения или тока;

- проверку баланса мощностей.

Рассеиваемая мощность Pk характеризует способность сопротивления rk (или проводимость gk) необратимо преобразовывать электрическую энергию в любой другой вид энергии и рассчитывается по одной из формул:

Суммарная рассеиваемая мощность для n сопротивлений и проводимостей определяется арифметической суммой мощностей, рассеиваемых в отдельных сопротивлениях rk или проводимостях gk цепи:

,

где 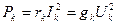- мощность, рассеиваемая в сопротивлении rk или проводимости gk, при этом направление напряжения или тока не влияет на рассеиваемую мощность.

В отличие от сопротивлений и проводимостей, которые способны только потреблять электрическую энергию, активные элементы (источники напряжения или тока) способны как потреблять, так и отдавать энергию во внешнюю цепь. В цепях с одним источником всегда происходит передача энергии источника во внешнюю цепь. При наличии в цепи нескольких источников некоторые из них могут работать в режиме потребления энергии. Такое положение может иметь место, например, при зарядке или разрядке аккумуляторов. В связи с этим мощность источников следует определять с учётом направлений напряжения и тока в них, пользуясь формулами:

или .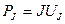

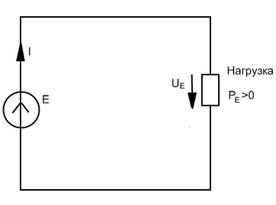
При положительных направлениях напряжения и тока источников, которые приведены на рис. 2.3, энергия источников передаётся во внешнюю цепь, и, следовательно, их мощность имеет положительное значение (). При отрицательных направлениях источники работают в режиме потребления энергии, и, следовательно, их мощность имеет отрицательное значение ().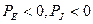

a) б)

Рис.2.3. К расчёту мощности источников напряжения (а) и тока (б)

Балансом электрических мощностей называют установление равенства мощностей, отдаваемых источниками во внешнюю цепь, и мощностей, потребляемых нагрузками.

Баланс мощностей можно установить с помощью формулы:

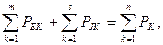
Где сравнивается сумма мощностей s источников тока Jk и m источников напряжения Ek (с учётом их знаков) с суммой мощностей Pk, потребляемых в n сопротивлениях rk или проводимостях gk цепи. При правильном решении задачи баланс мощностей соблюдается.

Пример 2.1. Требуется определить мощности источников энергии, мощности, рассеиваемые в сопротивлениях, и установить баланс мощностей для цепи, рассмотренной в примере 2.1. (рис.2.4.).

Рис.2.4.

Решение. Решение задачи будем основывать на значениях токов и напряжений, полученных при решении примера 2.1.

Вначале определим мощность, которую отдают в цепь источники напряжения:

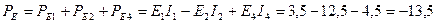Вт.

Из выполненного расчёта следует, что только источник E1 отдаёт энергию в цепь, а источники E2 и Е4 её потребляют.

Теперь определим суммарную мощность, которую отдают в цепь источники тока:

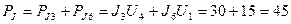Вт.

Из этого решения следует, что оба источника тока отдают энергию в цепь.

Полная мощность источников энергии:

Вт.

Наконец, определим мощность потерь в сопротивлениях цепи:

Вт.

Результаты расчёта показывают, что баланс мощностей выполняется.
Раздел 3.

Дата добавления: 2014-01-13