Метод узловых потенциалов (МУП)

Метод позволяет уменьшить количество уравнений системы до числа , где N_y – число узлов электрической схемы.

Сущность метода заключается в том, что сначала определяются потенциалы всех узлов схемы, а токи ветвей, соединяющих узлы, определяются с помощью законов Ома.

При составлении уравнений по МУП сначала полагают равным нулю потенциал какого-либо узла, для оставшихся 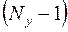составляют уравнения по I-му закону Кирхгофа.

Если в цепи некоторые узлы соединяются ветвями, не имеющими сопротивлений (они могут содержать источники напряжений), то число K_I уравнений, составленных по МУП, уменьшается на N_н (число ветвей с нулевыми сопротивлениями).

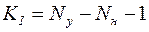- число уравнений по МУП.

Прежде, чем перейти к изложению самого метода, напомним, что в случае, когда между двумя узлами имеются несколько параллельных ветвей с источниками ЭДС (или без них), их можно привести к одной эквивалентной схеме.

Дальше будем предполагать, что 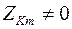, т.е. между узлами цепи не включены идеальные источники ЭДС.

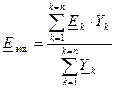
Это представление эквивалентной схемой параллельных ветвей с источниками ЭДС даёт нам право без ограничения общности считать, что между любой парой узлов включена только одна ветвь.

Первое уравнение Кирхгофа для некоторого узла К можно записать:

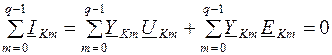(6.1)

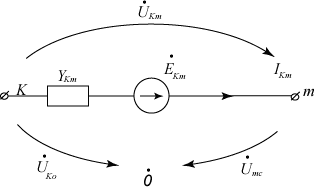
Рис.6.1.

Между узлами К и m имеется ветвь с источниками ЭДС (E _Km), сопротивлением Z _Km, то ток в этой цепи (ветви), направленный от К к m связан соотношениями:

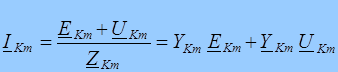(6.2)

Первый закон Кирхгофа для рис.6.1. имеет вид (6.2).

Напряжение можно выразить через узловые напряжения и 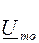в виде:

.

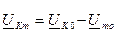Получаем:

или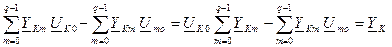

Обозначив 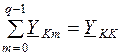, где Y _KK – сумма проводимостей всех ветвей, присоединённых к К -ому узлу, имеем:

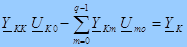- что и является основным уравнением для К -ого узла по МУП.

В развёрнутой форме совокупность уравнений по МУП имеет вид:

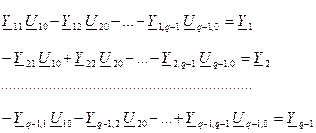
Решая эту систему, найдём узловые напряжения, причём для К -ого узла величина 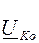будет:

,

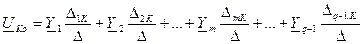где D - главный определитель системы, D _mK – его алгебраическое дополнение.

После того, как узловые напряжения найдены, определения токов в ветвях цепи имеют вид: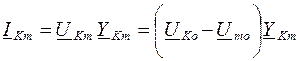

Если в ветви содержатся ЭДС, то ток равен:

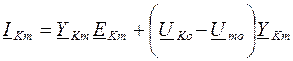
Метод узловых напряжений применяется к независимым узлам.

Если к К -ому узлу подтекает ток от источника тока, то он должен быть включен в ток I _KK со знаком «+», если утекает, то со знаком «-».

Если между какими-либо двумя узлами нет ветви, то соответствующая проводимость равна 0.

Y _ii – собственная проводимость всех ветвей, подходящих к узлу i (всегда со знаком «+»).

Y _iк – взаимная проводимость между узлами i и к (входит в уравнение всегда со знаком «-» при выбранном направлении всех узловых напряжений к базисному узлу).

Ток I ₁ называется узловым током 1-ого узла.

Это расчётная величина, равная алгебраической сумме токов, полученных от деления ЭДС ветвей, подходящих к 1-ому узлу, на сопротивления данных ветвей. В эту сумму со знаком «+» входят токи тех ветвей, ЭДС которых направлена к 1-ому узлу.

Y ₁₁ – проводимость всех ветвей, сходящихся в 1-ом узле.

Y ₁₂ – проводимость взаимная – равняется сумме проводимостей всех ветвей, соединяющих узел 1 с узлом 2 (берётся со знаком «-»).

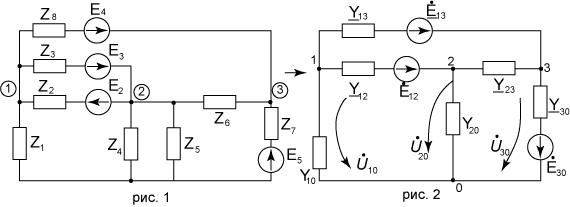
В качестве примера составим уравнение по МУП для электрической цепи, изображённой на рис. 3

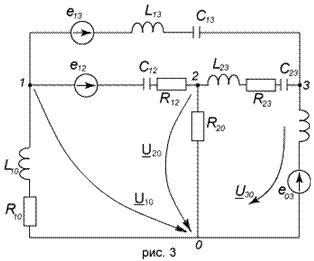Задано:

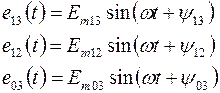
и параметры всех элементов.

Расчёт цепи производим комплексным методом:

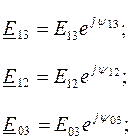
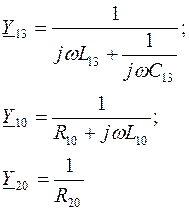
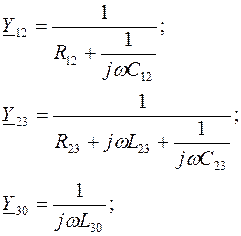
Для узлов 1, 2, 3 имеем уравнения:

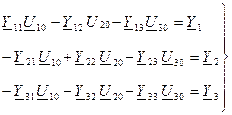(1)

Y ₁₁= Y ₁₂+ Y ₁₀+ Y ₁₃; Y ₂₂= Y ₂₀+ Y ₁₂+ Y ₂₃; Y ₃₃= Y ₃₀+ Y ₁₃+ Y ₂₃

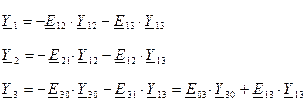
Решив систему из 3-х уравнений относительно узловых напряжений, находим напряжения на ветвях и токи в них. Метод узловых напряжений применим к независимым контурам.

Положительное направление всех узловых напряжений принято считать к опорному узлу.

Раздел 7.

Дата добавления: 2014-01-13