Код Шеннона-Фано

Оценка количества информации на выходе дискретного источника

Мера Шеннона

Мера Хартли

Мера количества информации, введенная Шенноном

I=log₂ M дв.ед./сообщение,

где M – количество состояний источника.

H=-Σp (i)*log₂ p(i) бит/сообщение,

где p(i) – вероятность появления i-го состояния (сообщения) на выходе источника

Количество информации на одно сообщение было названо Шенноном энтропией, т. к. формула Шеннона напоминала формулу оценки энтропии системы в физике.

Предположим, что источник информации имеет 4 состояния (4 буквы) и на выходе появилась последовательность букв:

…ВВОЗВНВОВНВОЗВОВЗНВОВНВОВОВВОВЗВНВЗВОВВ….

Можно определить, сколько раз встречается каждая из букв в последовательности и найти вероятность (частоту) появления каждой буквы.

Вероятность появления каждой буквы можно вычислить как отношение числа повторений буквы к общему количеству букв в фрагменте. Для получения более точных результатов следует брать достаточно длинные последовательности. В данном фрагменте текста всего 40 букв. Результаты расчета сведены в таблицу 1.

Таблица 1

Буква	Число повторений	Вероятность появления p(i)
В		0,5
О		0,25
Н		0,125
З		0,125

Если взять формулу Хартли, то количество информации на одну букву:

I=log₂ 4=2 дв.ед/букву

При расчете по формуле Шеннона получим:

H = - (0,5*log₂0,5 + 0,25*log₂0,25 + 0,125*log₂0,125 + 0,125*log₂0,125) =

-[ 0,5*(-1) + 0,25*(-2) + 0,125*(-3) + 0,125*(-3)]=1,75 бит/сообщение

Оценки количества информации по разным формулам дают разные результаты. Результаты будут одинаковыми, если вероятности событий на выходе источника будут равными.

Например

p(В) = 0,25,

p(О) = 0,25,

p(Н) = 0,25,

p(З) = 0,25.

H = - (0,25*log₂0,25 + 0,25*log₂0,25 + 0,25*log₂0,25 + 0,25*log₂0,25) =

-[(-0,5)+(-0,5)+(-0,5)+(-0,5)]=2 бит/сообщение

Формула Шеннона позволяет оценить информацию источника, состояния которого имеют разную вероятность.

Код был предложен для передачи информации источника, имеющего разные вероятности состояний.

В таблице 2 представлен алгоритм кодирования источника для рассмотренного выше примера.

Таблица 2

Буква	Вероятность p(i)	Ступени кодирования	Код	n(i)
В	0,5
О	0,25
Н	0,125
З	0,125

Для получения кодовых комбинаций следует выполнить последовательное деление букв в таблице на два подмножества, и каждому подмножеству присваивать определенный символ двоичного кода. Суммарные вероятности появления букв в каждом множестве должны быть приблизительно одинаковы. Деление продолжается, пока остается хотя бы одно подмножество, содержащее более одной буквы.

Можно подсчитать среднее количество бит для передачи одной буквы текста с учетом вероятности появления букв на выходе источника.

n=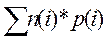

n=1*0,5 + 2*0,25 + 3*0,125 + 3*0,125 = 1,7 (бит/букву)

Например, текст содержит 1000 букв.

Для передачи этого текста равномерным двоичным кодом потребуется 2000 двоичных разрядов (2*1000).

При кодировании кодом Шеннона-Фано потребуется 1,7*1000=1700 двоичных разрядов. Таким образом, сообщение будет передано по каналу быстрее, чем при использовании равномерного кода.

Задача.

Отгадать последовательность переданных по двоичному каналу букв

Пропускная способность канала без шумов

C=(1/t)*log₂m бит/сек,

где t-время передачи сигнала,

m - количество дискретных состояний сигнала.

Дата добавления: 2014-01-13