Бесконечно большие и бесконечно малые функции

Основные теоремы о пределах функций.

1. Функция не может иметь более одного предела.

2. Предел суммы двух функций равен сумме пределов.

3. Предел произведения двух функций равен произведению пределов.

4. Предел произведения числа на функцию равен произведению числа на предел функции (постоянный множитель выносится за знак предела).

5. Предел отношения двух функций равен отношению пределов этих функций. (Кроме случая, когда знаменатель стремиться к нулю). Если знаменатель стремиться к нулю, а числитель - нет, то отношение стремиться к бесконечности.

Опр. 1. Функция f(x) называется бесконечно большой величиной при х 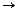а, если абсолютное значение остается большим любого заранее данного положительного числа М, всякий раз как абсолютное значение разности х-а меньше некоторого положительного числа 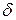(зависящего от М).

Опр. 2. Бесконечно малой величиной называется величина, предел которой равен нулю.

Основные свойства бесконечно малых величин:

1. Сумма двух бесконечно малых величин есть величина бесконечно малая.

2. Произведение ограниченной величины на бесконечно малую величину есть бесконечно малая величина. В частности, произведение постоянной величины на величину бесконечно малую, а также произведение бесконечно малых величин есть бесконечно малая величина.

3. Частное от деления бесконечно малой величины на переменную величину, стремящуюся к пределу, не равному нулю, есть бесконечно малая величина.

Из определений бесконечно большой и бесконечно малой величин следует, что если у – бесконечно большая величина, то бесконечно малая; если у – бесконечно малая величина, то бесконечно большая.

Дата добавления: 2014-01-13