Замечательные пределы

Есть особые случаи, когда предел суммы, произведения или частного нельзя найти, зная только пределы слагаемых, сомножителей или делимого и делителя. Такие случаи называются неопределенностями.

Выделяют неопределенности двух типов:

1. Арифметические неопределенности (0/0); (∞/∞); (∞ – ∞); (0 · ∞).

2. Степенно-показательные неопределенности (1^∞); (∞⁰); 0⁰.

Эти записи не являются операциями над числами и ∞, они представляют собой только деловые обозначения.

В случае неопределенности предел может быть равен нулю, конечному числу, бесконечности или не существовать. Для нахождения предела (раскрытие неопределенности) надо исследовать каждый случай отдельно.

Для раскрытия неопределенностей используются не только различные приемы преобразования функций, но и так называемые замечательные пределы.

Первый замечательный предел 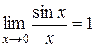, он раскрывает неопределенность (0/0).

Второй замечательный предел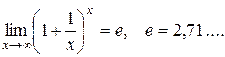

Дата добавления: 2014-01-13