Эквивалентные функции

Пусть α(х) и β(х) — бесконечно малые при х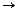а. Их частное может и не быть бесконечно малым. Более того, предел отношения двух бесконечно малых величин является неопределенной величиной 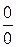. В зависимости от того, какие конкретные бесконечно малые рассматриваются, этот символ может быть равен произвольному числу, или символу бесконечности.

Опр. 1. Если отношение 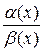двух бесконечно малых величин само бесконечно мало, то α(х) называется величиной более высокого порядка малости, чем β(х); при этом β(х) называется величиной более низкого порядка малости, чем α(х).

Если отношение 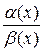двух бесконечно малых величин стремится к конечному пределу, не равному нулю, то α(х) и β(х) называются бесконечно малыми одного порядка малости. В частности, если отношение 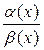двух бесконечно малых величин стремится к 1, то α(х) и β(х) называются эквивалентными. В этом случае пишут α(х) ~ β (х).

Таблица эквивалентных бесконечно малых функций. Пусть α(х) - бесконечно малая при х 0. Тогда

Принцип замены эквивалентных. Если функции α(х) и β(х) являются бесконечно малыми при ха и если α(х) ~ 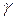(x), β (х) ~ 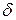(x), то

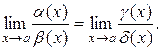
Дата добавления: 2014-01-13