Наклонные асимптоты

Примеры.

1. Найти вертикальные асимптоты графика функции .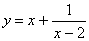

Так как 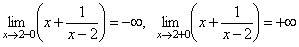, то прямая x = 2 является вертикальной асимптотой.

2. .

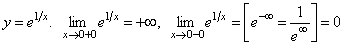Прямая x = 0 – вертикальная асимптота.

Поскольку асимптота – это прямая, то если кривая y = f(x) имеет наклонную асимптоту, то ее уравнение будет y = kx + b. Наша задача найти коэффициенты k и b.

Теорема. Прямая y = kx + b служит наклонной асимптотой при x → +∞ для графика функции y = f(x) тогда и только тогда, когда 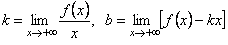. Аналогичное утверждение верно и при x → –∞.

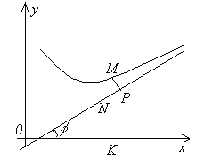
Доказательство. Пусть MP – длина отрезка, равного расстоянию от точки M до асимптоты. По условию 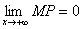. Обозначим через φ угол наклона асимптоты к оси Ox. Тогда из ΔMNP следует, что 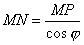. Так как φ постоянный угол (φ ≠ π/2), т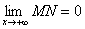о , но

MN = MK – NK = y - y _ас = f(x) - (kx+b).

Следовательно, мы можем записать следующее равенство .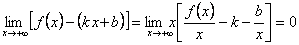

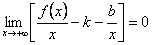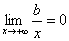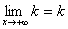Так как x → +∞, то должно выполняться равенство . Но при постоянных k и b и . Следовательно, 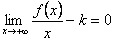, т.е. .

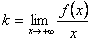Если число k уже известно, то 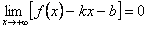, поэтому .

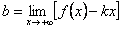Для доказательства в случае x → –∞ все рассуждения аналогичны.

Докажем обратное утверждение. Предположим, что существуют пределы, определяющие числа k и b. Тогда несложно заметить, что выполняется равенство 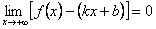. Действительно

Следовательно, прямая y = kx + b есть асимптота. Теорема полностью доказана.

Сделаем несколько замечаний.

Замечание 1. Теорема показывает, что для нахождения асимптот достаточно найти два указанных предела. Причем, если хотя бы один из пределов не существует или обращается в бесконечность, то кривая асимптот не имеет.

Замечание 2. В случае, когда k = 0 асимптота y = b называется горизонтальной асимптотой. Наличие горизонтальной асимптоты означает, что существуют пределы

.

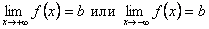Замечание 3. Пределы для отыскания k и b могут быть различны при x → +∞ и x → – ∞ и, следовательно, график функции может иметь две различные асимптоты при x → +∞ и x → –∞.

Примеры. Найти асимптоты кривых.

1. .

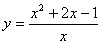1. Вертикальные:

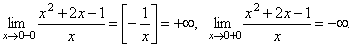
x = 0 – вертикальная асимптота.

2. Наклонные:

.

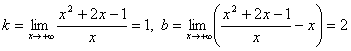При x → - ∞ получим те же значения k и b. Следовательно, прямая y = x + 2 является наклонной асимптотой.

2. y = e ^{– x} sin x + x.

1. Функция определена и непрерывна на всей числовой прямой, следовательно, вертикальных асимптот нет.

2.

а) .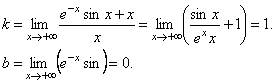

Итак, при x → +∞ наклонная асимптота у = х.

б) 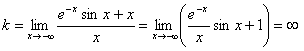, т. к.

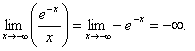, поэтому при x → - ∞ наклонных асимптот нет.

3. y = x – 2arctg x.

1. Вертикальных асимптот нет.

2.

а) .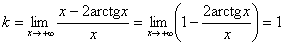

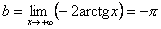. Наклонная асимптота y = x – π при .

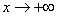б) 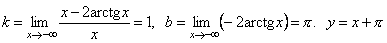при .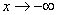

Дата добавления: 2014-01-13