
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Частные производные. Полный дифференциал
Опр. 1. Множество точек М, которые удовлетворяют неравенству 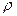 (М; М
(М; М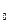 )<
)<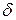 , называют
, называют 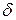 - окрестностью точки М
- окрестностью точки М 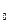 .
.
Пусть функция двух переменных z=f (x; у) (для большего количества переменных всё аналогично) определена в некоторой окрестности точки М (x; у). Дадим переменной х приращение 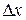 так, чтобы точка (х+
так, чтобы точка (х+ 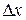 ; у) принадлежала этой окрестности. При этом функция z=f (x; у) изменится на величину
; у) принадлежала этой окрестности. При этом функция z=f (x; у) изменится на величину  , которая называется частичным приращением функции z=f (x; у) по переменной х.
, которая называется частичным приращением функции z=f (x; у) по переменной х.
Аналогично величину 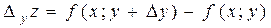 называют частичным приращением функции по переменной у.
называют частичным приращением функции по переменной у.
Опр. 2. Если существует предел 
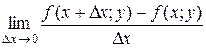 , то его называют частной производной функции z=f(x;у) в точке М (x;у) по переменной х и обозначают такими символами:
, то его называют частной производной функции z=f(x;у) в точке М (x;у) по переменной х и обозначают такими символами: 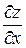 ,
, ,
, ,
,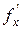 .
.
Аналогично 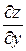 =
= 
 .
.
Из таких определений следует, что правила вычисления производных, совпадают с правилами дифференцирования функций одной переменной. Следует только помнить, что при вычислении частной производной по одной переменной остальные переменные считаются постоянными.
Частные производные характеризуют скорость изменения функции в направлении соответствующих координатных осей.
Опр. 3. Частные производные от частных производных 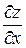 ,
, 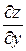 функции z=f (x; у) называются частными производными второго порядка. Функция двух переменных может иметь четыре частные производные второго порядка, которые обозначают так:
функции z=f (x; у) называются частными производными второго порядка. Функция двух переменных может иметь четыре частные производные второго порядка, которые обозначают так:
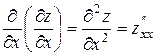 ,
, 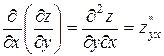 ,
,
 ,
, 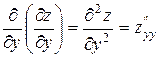 .
.
Производные  и
и  называются смешанными. Можно доказать, что если они непрерывны, то равны между собой.
называются смешанными. Можно доказать, что если они непрерывны, то равны между собой.
Частные производные от частных производных второго порядка называются частными производными третьего порядка и т. д.
Пусть функция z=f (x; у) непрерывна в некоторой окрестности точки М (x; у) вместе со своими частными производными 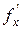 (х; у) и
(х; у) и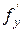 (х; у). Выберем приращение
(х; у). Выберем приращение 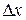 и
и  так, чтобы точка (х+
так, чтобы точка (х+ 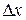 ;у+
;у+ ) принадлежала рассматриваемой окрестности.
) принадлежала рассматриваемой окрестности.
Опр. 4. Если полное приращение функции z=f (x; у) в точке М (x; у) 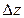 = f (x+
= f (x+ 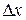 ; у +
; у + )– f (x; у) можно записать в виде
)– f (x; у) можно записать в виде 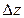 =
=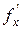 (х; у)
(х; у)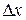 +
+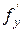 (х; у)
(х; у) +
+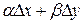 , где
, где  – бесконечно малые функции при
– бесконечно малые функции при 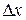
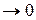 ,
, 
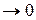 , то функция z=f (x; у) называется дифференцируемой в точке М (x; у), а линейная относительно
, то функция z=f (x; у) называется дифференцируемой в точке М (x; у), а линейная относительно 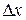 и
и  часть её полного приращения
часть её полного приращения 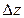 называется полным дифференциалом функции и обозначается dz=
называется полным дифференциалом функции и обозначается dz= 
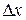 +
+
 .
.
Дифференциалами независимых переменных называют приращения этих переменных dх= 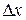 , dу=
, dу=  . Поэтому dz=
. Поэтому dz=  dх +
dх + dу, или в других обозначениях dz=
dу, или в других обозначениях dz= 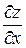 dх +
dх +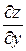 dу.
dу.
Для функции трёх переменных и=f (x; у; z) dи= 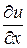 dх +
dх +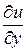 dу+
dу+  dz.
dz.
Полный дифференциал функции z=f (x; у) dz= 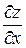 dх +
dх +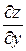 dу,который ещё называют дифференциалом первого порядка, зависит от независимых переменных х, у и от их дифференциалов dх, dу. Заметим, что дифференциалы dх, dу не зависят от х, у.
dу,который ещё называют дифференциалом первого порядка, зависит от независимых переменных х, у и от их дифференциалов dх, dу. Заметим, что дифференциалы dх, dу не зависят от х, у.
Дифференциалы второго порядка определяют по формуле d2z=d (dz).
Тогда
d2z=d (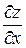 dх+
dх+ 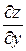 dу)=
dу)= (
(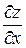 dх+
dх+ 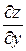 dу) dх+
dу) dх+  (
(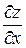 dх+
dх+ 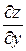 dу) dу=
dу) dу=
=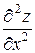 dх2+
dх2+  dуdх+
dуdх+  dхdу+
dхdу+ 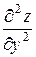 dу2,
dу2,
откуда d2z= 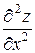 dх2+ 2
dх2+ 2 dхdу+
dхdу+ 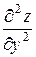 dу2.
dу2.
Символически это можно записать так: d2z= ( dх+
dх+  dу)2 z.
dу)2 z.
Аналогично можно получить формулу для полного дифференциала п -го порядка: dпz=d (dп-1z)=( dх+
dх+  dу) пz.
dу) пz.
|
|
Дата добавления: 2014-01-13; Просмотров: 866; Нарушение авторских прав?; Мы поможем в написании вашей работы!