Относительный покой жидкости. Под относительным покоем понимают неподвижное состояние жидкости относительно сосуда, который движется с постоянным ускорением

Под относительным покоем понимают неподвижное состояние жидкости относительно сосуда, который движется с постоянным ускорением. Например, в относительном покое может находиться жидкость в емкости, которая установлена на разгоняющейся транс­портной машине (топливный бак автомобиля). В относительном покое будет также находиться жидкость в сосуде, вращающемся с постоянной скоростью.

Законы, действующие при относительном покое жидкости, принципиально не отличаются от ранее рассмотренных законов гидростатики. Но если в ранее рассмотренных случаях на жидкость действовала только одна массовая сила — сила тяжести, то при относительном покое появляет­ся новая — сила инерции. Это приводит к изменению положе­ния свободной поверхности жид­кости и изменению давлений в различных ее точках.

Анализ относительного по­коя удобно проводить для сил, действующих на условную частицу жидкости единичной мас­сы (массой m = 1). При таком подходе сила всегда численно равна соответствующему уско­рению. Например, на частицу единичной массы действует сила тяжести G=m=1g=g. Таким образом, математические зависимости существенно упрощаются.

Рассмотрим прямолинейное движение сосуда с постоянным ус­корением

(или замедлением) а. В этом случае на каждую частицу жидкости

единичной массы действуют две силы: сила тяжести g и сила инерции а (рис. 2.7). Равнодействующая этих двух сил

j = 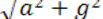(2.10)

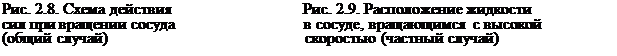
определяет положение свободной поверхности жидкости, так как угол между этой поверхностью и силой j всегда составляет 90°. Из геометрических соображений (см. рис. 2.7) следует, что положение свободной поверхности может быть задано углом а, значение ко­торого найдем из отношения

tga = a/g.

Для определения давления в произвольно выбранной точке на расстоянии от свободной поверхности используется математи­ческая зависимость

p = 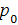+lpj (2.11)

Учитывает действие не только сил тяже­сти, но и сил инерции.

Эта зависимость является более общей, чем основной закон Гидростатики, который может быть получен из нее как частный случай. Действительно, при а = 0 из (2.10) следует j = g. Тогда с учетом l=h из (2.11) получим формулу (2.1), т.е. основной закон гидростатики.

Другим случаем относительного покоя жидкости является вра­щение сосуда с постоянной угловой скоростью ω (рис. 2.8). При вращении на каждую частицу жидкости единичной массы, распо­ложенную на радиусе r, также действуют две силы: сила тяжести g и сила инерции, вызванная центробежным ускорением, а = ω²r. Равнодействующая этих двух сил

j =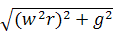

определяет положение свободной поверхности жидкости. Но в рас­сматриваемом случае центробежное ускорение является перемен­ной величиной, так как зависит от радиуса расположения точки. Поэтому поверхность вращения принимает параболическую фор­му и описывается уравнением

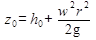
где Zo — высота расположения точки свободной поверхности отно­сительно дна сосуда; h₀ — высота жидкости на оси вращения.

Формула для определения давления р в любой точке жидкости может быть получена методом, использованным в подразд. «Свойства гидростатического давления и основной закон гидростатики». Тог­да после математических преобразований найдем давление в точ­ке, расположенной на радиусе г и высоте z относительно дна со­суда:

P=Po+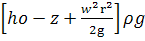 (2.12)

Из формулы (2.12), так же как и из (2.11), можно получить основной закон гидростатики как частный случай, если принять ω = 0 и обозначить h= h₀- z.

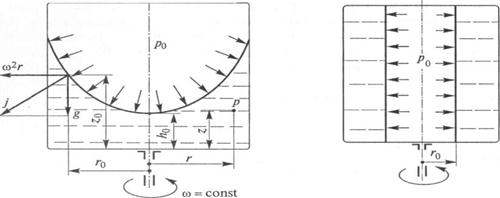
На практике часто встречается другой частный случай — вра­щение сосуда с очень высокой скоростью. В этом случае центро­бежные силы существенно больше сил тяжести и жидкость отбра­сывается центробежными силами к стенкам сосуда (рис. 2.9), а ее свободная поверхность располагается на радиусе г₍₎. Тогда некото­рыми геометрическими величинами, входящими в (2.12), можно пренебречь и формула для определения давления упрощается:

(2.13)

Следует отметить, что формула (2.12) получена для сосуда, имеющего вертикальную ось вращения, а формула (2.13) приме­нима для вращающихся сосудов с любым расположением оси в пространстве.

Дата добавления: 2014-01-13