Сила давления на криволинейные стенки. Плавание тел

Рассмотрим силу, действующую на криволинейную цилиндри­ческую стенку, которая погружена в жидкость так, что ее образу­ющие параллельны свободной поверхности жидкости (рис. 2.5). Такие стенки распространены на практике. В этом случае задача может быть сведена к определению равнодействующей силы, ле­жащей в вертикальной плоскости, перпендикулярной образующим цилиндрической поверхности. Определение этой силы сводится к определению ее вертикальной и горизонтальной составляющих.

В пределах цилиндрической поверхности (см. рис. 2.5) выделим участок А В и найдем силу F, действующую на этот участок при условии, что на свободной поверхности жидкости существует дав­ление р₀. Причем определим эту силу для двух случаев: жидкость расположена над цилиндрической поверхностью (см. рис. 2.5, а) и под ней (см. рис. 2.5, б). При определении силы, действующей на стенку, будем учитывать, что со стороны стенки на жидкость дей­ствует такая же сила, но в противоположном направлении.

Для определения силы F в первом случае (см. рис. 2.5, а) выде­лим объем жидкости, ограниченный поверхностью АВ и вертикаль­ными плоскостями, проходящими через границы выбранного уча­стка. На рис. 2.5, а эти плоскости отображены линиями AL и ВК. Рассмотрим условия равновесия выделенного объема в вертикальном

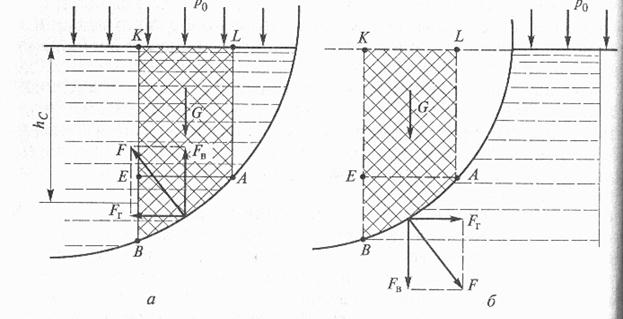
Рис. 2.5. Схема расположения силы давления на криволинейную поверхность в случае расположения жидкости над (а) и под (б) криволинейной поверхностью

и горизонтальном направлениях, из которых найдем верти­кальную F_B и горизонтальную F_r составляющие силы F.

На выделенный объем жидкости в вертикальном направлении, кроме силы F_B, действуют его вес G и сила давления на свобод­ную поверхность, равная произведению давления р₀ на площадь горизонтальной проекции поверхности АВ, обозначаемую S_r. Тог да из условия равновесия найдем вертикальную составляющую

F_B = p₀S_r+G. (1.5)

При рассмотрении условия равновесия в горизонтальном на­правлении будем считать, что силы, действующие на поверхност ЕК и AL, взаимно уравновешены. Следовательно, на выделенны объем жидкости в горизонтальном направлении, кроме искомо силы F_r, действует только сила давления на площадь вертикально проекции поверхности АВ, обозначаемую S_B. Ее найдем по форму­ле (2.4):

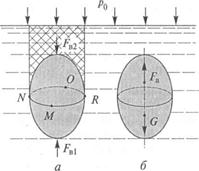F_r = 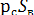= (Ро + hcPg)S_e, (2.6)

где И_с — глубина погружения центра тяжести поверхности АВ; 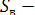площадь поверхности BE.

Определив по формулам (2.5) и (2.6) вертикальную F_B и гори­зонтальную F_T составляющие силы F, найдем ее численное значе­ние по зависимости

F =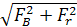 (2.7)

Зависимости (2.5)...(2.7) получены для случая с расположением жидкости над криволинейной поверхностью. Очевидно, что при

расположении жидкости снизу относительно стенки (см. рис. 2.5, б) давления в соответствующих точках будут точно такими, как и в первом случае. Поэтому и силы, действующие на стенку (полная сила и ее вертикальная и горизонтальная составляющие), будут такими же по значению. Но направления этих сил будут противо­положными, так как жидкость действует

на стенку с обратной сто­роны. Таким образом, формулы (2.5)...(2.7) будут справедливы и для этого случая. При этом в формулу (2.5) входит та же величина G, т.е. вес жидкости, которая заняла бы объем ABKL (выделен на рис. 2.5, б). Полученные зависимости справедливы для цилиндрической

поверхности, которая погружена в жидкость так, что ее образу­ющие параллельны свободной поверхности. Аналогичным образом могут быть получены формулы для произвольной криволинейной поверхности. Их отличие будет в том, что полная сила F будет равна векторной сумме не двух составляющих сил (как в предыду­щем случае), а трех. Причем одна из этих составляющих будет вер­тикальной, а две — горизонтальными и взаимно-перпендикулярными.

Важной задачей при решении некоторых практических вопро­сов является определение силы, выталкивающей тело, погружен­ное в жидкость. На рис. (2.6, а) изображено тело произвольной формы, погруженное в жидкость. Рассмотрим силы, действующие на это тело в вертикальном на­правлении.

При рассмотрении сил, дей­ствующих на тело, условно разде­лим его замкнутой линией MNOR на две части: верхнюю и нижнюю. Причем линия разделения MNOR проведена так, что ее проекция и проекция тела на свободную поверхность жидкости (т. е. верти­кально вверх) полностью совпа­дают. Обозначим вес жидкости, расположенной над телом, G₀ (на рис. 2.6, а выделена штриховкой), а вес жидкости, вытесненной телом, — G, т. е. это вес жидкости, которая заняла бы объем погруженного тела (на рис. 2.6, а выделен затемнением).

Вертикальную силу (см. рис. 2.6, а), действующую на нижнюю поверхность тела, определим с использованием формулы (2.5):

F_Bl=p₀S_r + G₀+G, (2.8)

где S_r — площадь горизонтальной проекции тела на свободную по­верхность жидкости.

Таким же образом найдем вертикальную силу (см. рис. 2.6,а), действующую на верхнюю часть тела:

F_в2=PoS_r + G₀. (2.9)

Их равнодействующая сила F_a, направленная вверх, будет рав­на алгебраической сумме этих сил и с учетом (2.8) и (2.9) опреде­ляется по формуле

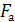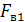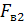= - = G.

Силу F_a принято называть архимедовой силой, а полученную для ее определения зависимость — законом Архимеда, согласно которому на тело, погруженное в жидкость, действует выталкива­ющая сила, направленная вверх и равная весу жидкости, вытес­ненной телом.

Точкой приложения этой силы является геометрический центр тела, который называется центром водоизмещения. Он может не совпадать с центром тяжести тела. Эти центры совпадают, если тело состоит из однородного и равномерно распределенно­го вещества. Плавающее тело будет находиться в устойчивом рав­новесии, когда центр водоизмещения располагается выше центра тяжести тела и они лежат на одной вертикальной прямой (см. рис. 2.6, б).

Дата добавления: 2014-01-13