Непрерывность функции

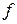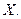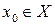Рассмотрим функцию , определенную на промежутке Пусть . Функция 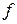называется непрерывной в точке 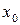, если

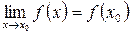
Функция 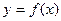называется непрерывной слева (справа) в точке 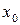, если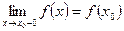 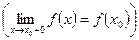. Естественно, при этом функция 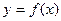должна быть определена в некоторой окрестности слева (справа) то точки 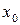. Непрерывность функции в точке 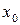означает непрерывность этой функции в указанной точке как слева, так и справа.

Функция 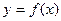, определенная на интервале 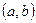называется непрерывной на интервале 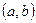, если она непрерывна в каждой точке 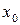этого интервала .

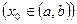Функция 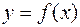, определенная на отрезке 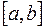(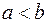) называется непрерывной на отрезке 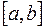, если она непрерывна в каждой точке 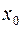интервала 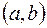, непрерывна справа в точке 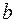и непрерывна слева в точке .

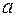Общие свойства непрерывных функций, заданных на отрезке 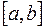, определяются четырьмя теоремами: двумя теоремами Больцано–Коши и двумя теоремами Вейерштрасса.

Теорема (первая теорема Больцано–Коши). Пусть функция 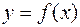определена и непрерывна на отрезке 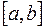, и на концах этого промежутка принимает значения разных знаков; тогда найдется точка 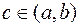, в которой функция равна нулю.

Теорема (вторая теорема Больцано–Коши). Пусть функция 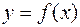определена и непрерывна на отрезке 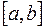. Тогда, если 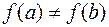то функция принимает все свои промежуточные значения, принадлежащие промежутку 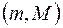, где 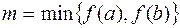, , 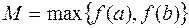т.е. .

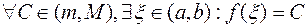Теорема (первая теорема Вейерштрасса). Пусть функция 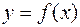определена и непрерывна на отрезке 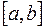, тогда функция 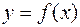является ограниченной на этом отрезке.

Теорема (вторая теорема Вейерштрасса). Пусть функция 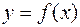определена и непрерывна на отрезке 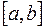, тогда функция 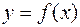имеет минимум и максимум на этом отрезке (множество значений функции включает в себя точные верхнюю и нижнюю границы).

Отметим прежде всего, что основные элементарные функции непрерывны во всех точках, в которых они определены. К основным элементарным функциям относятся:

1. Постоянная функция 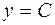. Область определения .

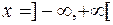2. Идентичная функция 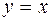. Область определения .

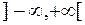3. Одночлен , .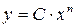

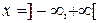4. Многочлен , .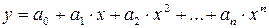

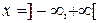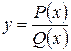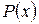5. Рациональная функция , где и 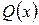‑ многочлены. Функция определена при всех 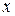, кроме корней многочлена .

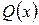6. Степенная функция 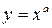. Если 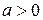, то функция определена по крайней мере на 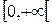. При 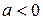определена по крайней мере на 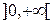. (При некоторых 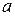степенная функция может быть определена на более широком множестве. Например, функция 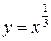имеет область определения 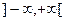. Функция 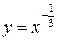определена на ).

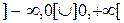7. Показательная функция 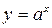, , 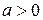. Определена на .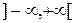

8. Логарифмическая функция 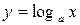, , 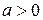. Определена на.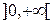

9. Синус 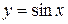, косинус 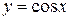определены на 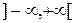. Эти функции являются периодическими с периодом 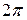, т.е. , для любого 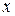из .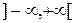

10. Арксинус 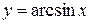и арккосинус 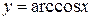определены на .

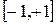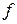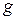Если и ‑ непрерывные функции, то их сумма, разность и произведение являются непрерывными функциями. Частное непрерывных функций 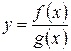будет непрерывно всюду, где оно определено. Таким образом, можно утверждать, что всякая арифметическая комбинация непрерывных функций непрерывна всюду, где она определена.

Дата добавления: 2014-01-13