Локальный экстремум функции нескольких переменных. Необходимое и достаточное условия. Исследование стационарных точек

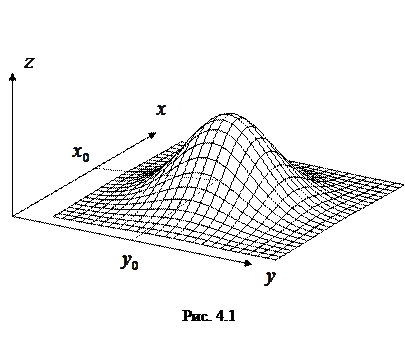
Пусть функция определена и непрерывна в области 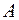. Локальным максимумом этой функции называется внутренняя точка у которой существует такая ненулевая – окрестность 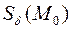для каждой точки 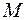из которой выполняется условие: .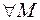

Если каждой точки 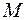из ненулевой – окрестности точки выполняется условие 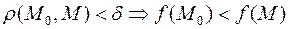, то точка называется локальным минимумом функции .

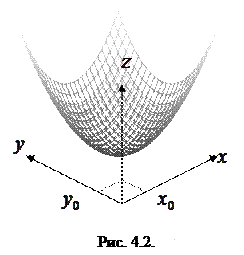
Точки локального минимума или максимума называются точками локального экстремума. Для этих точек характерно знакопостоянство величины абсолютного приращения 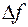в пределах ненулевой – окрестности. Для определения необходимого и достаточного признаков экстремальности функции предположим, что функция в области 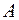не имеет точек разрыва и обладает дифференцируемостью до второго порядка. Как было указано выше, разложение абсолютного приращения 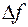имеет вид:

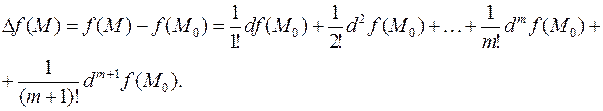Главный член разложения полного приращения является знакопеременным, так как линейно зависит от приращений 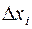. Поэтому в точке у функции не может наблюдаться экстремума, если вектор–градиент этой функции точке будет отличен от нулевого вектора, т.е. хотя бы одна из частных производных не будет равна нулю. Таким образом, необходимым условием существования локального экстремума функции является условие или

.

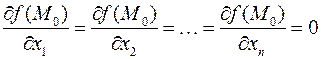Точки, в которых первые частные производные функции равны нулю или не существуют, называются критическими для данной функции. Критические точки, в которых первые частные производные функции существуют, называются стационарными. Функция многих переменных может достигать своего локального экстремума только в своей критической точке.

При обосновании достаточного условия существования экстремума введем дополнительное требование к функции : эта функция должна иметь непрерывные производные второго порядка в ненулевой – окрестности точки . Тогда условием наличия локального экстремума в критической точке или условием знакопостоянства абсолютного приращения 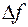в этой точке будет требование знакопостоянства второго слагаемого в разложении 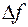, т.е. 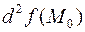. Влияние третьего и последующих членов разложения в этом случае будет пренебрежимо малым. Если формулу для вычисления 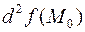сгруппировать и представить виде квадратичной формы:

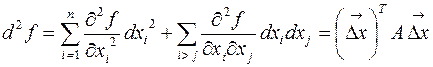
то требование знакопостоянства 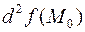сводится к требованию знакоопределенности матрицы квадратичной формы 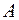в критической точке . В этом случае, если матрица квадратичной формы является положительно определенной, то в точке функция имеет локальный минимум, а если матрица 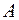отрицательно определена – то локальный максимум.

Условие знакопостоянства полного относительного приращения 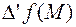выполняется в точках локальной выпуклости, определение которых можно дать по аналогии с функциями одной переменной.

Точка называется точкой локальной выпуклости функции , непрерывной и дифференцируемой в области 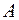, если она является внутренней точкой этой области и в некоторой ненулевой –окрестности точки выполняется условие: 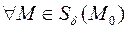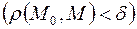полное относительное приращение 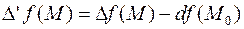знакопостоянно.

Если , точка называется точкой выпуклости вниз.

Если 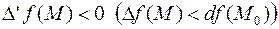, точка называется точкой выпуклости вверх.

Если условие локальной выпуклости вверх или вниз выполняется во всех точках области 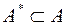, то функция называется однообразно выпуклой на области .

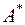Достаточным условием существования локальной выпуклости функции нескольких переменных в точке является знакопостоянство полного дифференциала второго порядка этой функции. Это несложно показать, воспользовавшись формулой разложения

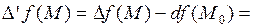
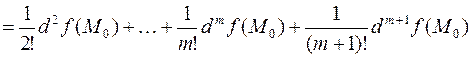
и проведя рассуждения аналогичные доказательству достаточного условия существования локального экстремума. Таким образом, знакопостоянство полного относительного приращения функции в некоторой ненулевой –окрестности точки определяется знакопостоянством полного второго дифференциала функции в точке .

Если , то функция имеет в точке локальную выпуклость вниз. Если 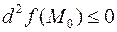, то функция имеет в точке локальную выпуклость вверх. Достаточное условие существования локального экстремума в критической точке кроме необходимого признака включает в свой состав требование наличия локальной выпуклости в этой точке.

Дата добавления: 2014-01-13