Интегрирование по частям. Если функции и дифференцируемы на множестве и, кроме того, на этом множестве существует интеграл

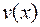Если функции и дифференцируемы на множестве 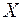и, кроме того, на этом множестве существует интеграл , то на нем существует и интеграл 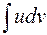, причем .

Действительно, если проинтегрировать формулу нахождения дифференциала произведения двух функций

,

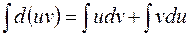то можно получить следующее соотношение между первообразными от этих функций

.

Такой способ нахождения интеграла называется интегрированием по частям. Этот способ целесообразно применять, если интеграл, стоящий в правой части проще исходного. При использовании метода интегрирования по частям задана левая часть равенства, т.е. функция и дифференциал . Таким образом, выбор функций и 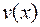неоднозначен, причем не каждый способ выбора этих функций ведет к упрощению первоначального интеграла.

Функции, интегрируемые по частям, можно схематично разделить на три группы.

1. Интегралы, подынтегральная функция которых содержит в качестве множителя одну из следующих 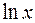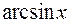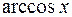функций: , , , , , , при условии, что оставшаяся часть подынтегральной функции представляет собой производную известной функции.

В случае если подынтегральная функция содержит в качестве множителя одну из перечисленных выше функций в степени 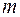, то операцию интегрирования по частям придется повторять 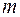раз.

2. Интегралы, подынтегральная функция которых содержит в качестве множителя одну из следующих функций: , , , 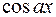a также, полином й степени

Для вычисления интегралов второй группы нужно формулу интегрирования по частям применять раз, причем в качестве функции нужно брать многочлен соответствующей степени. После каждого интегрирования степень полинома будет понижаться на единицу.

3. Интегралы вида:

; ; .

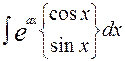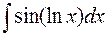Применение формулы интегрирования по частям может привести к ситуации, когда интеграл в правой части и интеграл в левой части равенства совпадают, т.е. получается равенство вида:

,

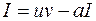где исходный интеграл;

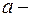постоянная .

В этом случае применение метода интегрирования по частям позволяет получить уравнение первого порядка для 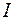, из решения которого находится исходный интеграл :

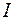Причем метод интегрирования по частям может применяться многократно и любой из сомножителей можно всякий раз принимать за .

Большое количество интегралов, не входящих в эти три группы, у которых невозможно выделить общий признак для группировки, также вычисляются методом интегрирования по частям. К таким интегралам можно отнести:

, , , ,

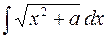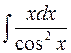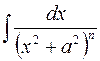
и многие другие.

Дата добавления: 2014-01-13