Механика

КГТУ им. А.Н. Туполева

Рекомендовано к изданию Учебно – методическим центром

Издательство Казан. гос. техн.ун-та, 2000

Ф.М.Гайсин, Б.А.Тимеркаев, Т.Я.Асадуллин, Д.Г.Галимов, Н.Ш.Гайнуллина, Н.К.Морозова, Х.М.Шавалиев, О.А. Петрова 2004

1. НЕКОТОРЫЕ СВЕДЕНИЯ О ВЕКТОРАХ.

1. Определение вектора.

Векторами называются величины, имеющие не только численное значение, но и определенное направление. Кроме того, векторы должны складываться по правилу параллелограмма.

Скалярные величины не связаны с направлением и обладают лишь численным значением.

Численное значение вектора называется его модулем. Модуль вектора - скаляр, причем всегда положительный.

На чертежах векторы изображаются в виде прямолинейных отрезков со стрелкой на конце. Длина отрезка определяет в установленном масштабе модуль вектора, а стрелка указывает направление вектора.

При печати векторы обычно обозначают буквами жирного шрифта, например, а, в, F и т. д. Для обозначения модуля вектора используется та же буква, только обычного шрифта. Например, а есть модуль вектора а. Иногда для обозначения модуля пользуются символом вектора, заключенным между двумя вертикальными черточками: ½ a ½= а - модуль вектора а.

Также векторы часто обозначаются буквами со стрелкой над ними, например 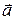. В этом случае та же буква без стрелки означает модуль вектора. Обозначение модуля вектора 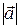= а тоже используется. В данном пособии мы будем использовать обозначение вектора буквой со стрелкой. Причем именно стрелкой, а не черточкой над буквой, так же буквой с черточкой над ней обозначается среднее (усредненное) значение данной величины.

Векторы могут быть отложены из любой точки пространства, а также перенесены параллельно себе в любую точку пространства. Совпадающие по модулю параллельные векторы, имеющие одинаковое направление, считаются равными друг другу.

2. Сложение и вычитание векторов.

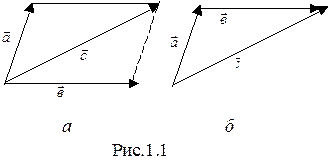Как уже говорилось выше, векторы складываются по правилу параллелограмма. На рис.1.1.а) показан результат сложения векторов и 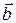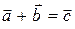. На рис. 1.1.б) видно, что такой же результат достигается при параллельном переносе вектора 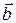, чтобы его начало совпало с концом вектора 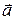. Последним способом особенно удобно графически складывать большое количество векторов(больше чем два).

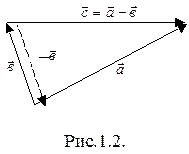Разностью векторов 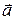и 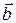называется такой вектор 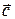, который в сумме с вектором 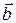дает вектор 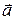. Графически разность векторов находится как изображено на рис. 1.2. Необходимо совместить начала векторов 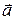и 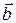, тогда начало вектора разности 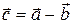будет на конце вектора 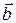а конец 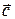будет на конце вектора .

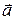Может быть кому-то более удобным покажется другой способ. Тот же результат получается если сложить вектор с вектором 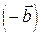(он изображен штриховой линией на рис.2.), который отличается от вектора 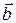противоположным направлением. Попробуйте сделать это самостоятельно.

3. Умножение вектора на скаляр.

В результате умножения вектора на скаляр a получается новый вектор 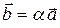, модуль которого в ½a½ раз больше, чем модуль вектора (b = çaç a). Направление вектора 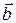либо совпадает с направлением вектора (если a>о), либо противоположно направлению вектора (если a< о). Умножение вектора на -1 изменяет направление вектора на обратное (вектор 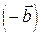на рис. 1.2).

Из определения операции умножения вектора на скаляр следует, что всякий вектор можно представить в виде 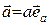, где а - модуль вектора , 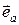- вектор с модулем равным единице, имеющий такое же направление как и . Вектор 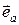называется единичным вектором или ортом вектора . Орт можно представить в виде 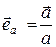, откуда следует, что орт является безразмерной величиной. Орты можно сопоставить не только вектором, но и любым направлениям в пространстве. Например, 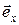есть орт координатной оси x, 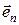- орт нормали к кривой или поверхности (нормаль - перпендикуляр, восстановленный из данной точки кривой или поверхности), - орт касательной к кривой и т. д.

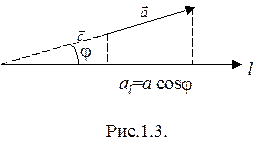4. Проекция вектора.

Рассмотрим некоторое направление в пространстве, которое мы зададим осью l (рис.1.3). Пусть вектор образует с осью l угол a. Величина a_l = а cosj, (где a - модуль вектора ) называется проекцией на ось l. Проекция обозначается той же буквой, что и вектор, с добавлением индекса, указывающего направление, на которое спроектирован вектор.

Проекция вектора есть величина алгебраическая. Если вектор образует с данным направлением острый угол, то cosj >0, так что проекция положительна, если угол j - тупой, то cosj <0 и, следовательно, проекция отрицательна. Когда вектор перпендикулярен к данной оси, проекция равна нулю.

5. Выражение вектора через его проекции на координатные оси.

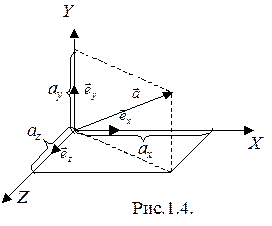В декартовой (прямоугольной) системе координат направления координатных осей x, y, z задаются ортами 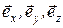. Эта тройка векторов полностью определяет систему координат и называется базисом координатной системы (рис. 1.4). На рис. 4 изображен вектор , отложенный из начала координат, который имеет проекции a_x, a_y, a_z на соответствующие оси. Можно показать, что любой вектор однозначно определяется следующим образом

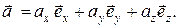
(Задание: сложите графически три вектора в правой части равенства и получите ). Поэтому a_x, a_y, a_z равны (с точностью до знака) сторонам прямоугольного параллелепипеда, большой диагональю которого служит вектор (построить самостоятельно).

Поэтому имеет место соотношение для модуля

a² = a_x² + a_y² + a_z².

Пусть 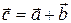. Тогда, выразив каждый вектор через его проекции, получим

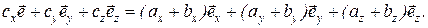
Равные векторы имеют равные проекции на координатные оси. Поэтому

c_x = a_x + b_x, c_y = a_y + b_y, c_z = a_z+ b_z.

Эти формулы справедливы при любом числе слагаемых векторов.

6. Скалярное произведение векторов.

Два вектора и 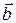можно умножить друг на друга двумя способами; один способ приводит к скалярной величине, другой дает в результате некоторый новый вектор. В соответствии с этим существует два произведения векторов - скалярное и векторное. Отметим, что операции деления вектора на вектор не существует. Скалярным произведением векторов 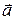и 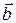называется скаляр, равный произведению модулей этих векторов на косинус угла a между ними:

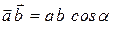(рис. 1.5)

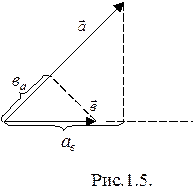Никакого знака между символами векторов не ставится. Скалярное произведение векторов иногда обозначают (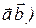или (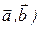всегда только в круглых скобках.

Если a острый 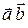>0, если a - тупой 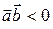. Если a =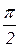(векторы перпендикулярны), то 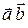= 0. Под квадратом вектора понимают скалярное произведение вектора самого себя:

(a = 0, cosa = 1).

Квадрат вектора равен квадрату его модуля. Квадрат орта равен 1. Скалярное произведение не зависит от порядка сомножителей:

.

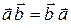Его можно записать несколькими способами

.

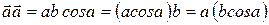Из рис. 1.5 видно, что a cosa = a_b - проекция вектора на направление вектора 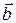. Аналогично b cosa = b_a - проекция вектора 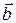на направление вектора . Поэтому

.

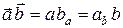Можно показать, что

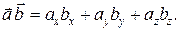
В свою очередь проекции вектора на оси координат в виде скалярного произведения вектора и соответствующего орта

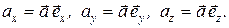
7. Векторное произведение.

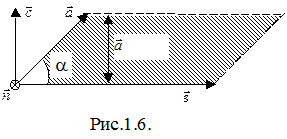Векторным произведением векторов 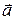и 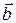называется вектор 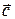, определяемый формулой 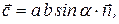где a и b- модули перемножаемых векторов, a - угол между векторами, 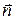- единичный вектор нормали к плоскости, в которой лежат векторы 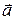и 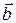(рис.1.6). Направление 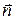выбирается так, чтобы последовательность векторов 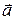, 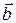и 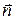образовывала правовинтовую систему. Это означает, что, если смотреть вслед вектору 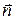, то совершаемый по кратчайшему пути поворот от первого сомножителя ко второму осуществляется по часовой стрелке. На рис. 1.6 вектор 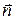направлен за чертеж и поэтому изображен кружкам с крестиком. Направление вектора 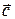совпадает с направлением .

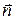Векторы, направленные от нас (за плоскость чертежа) обозначаются либо крестиком, либо кружочком с крестиком, а векторы, направленные на нас (из-за плоскости чертежа) обозначаются либо точками, либо кружочками с точкой. Это делается потому, что для наглядности вектор можно представить себе в виде стрелы с крестообразным оперением на хвосте. Когда стрела летит на нас, то мы видим наконечник - точку, а когда она летит от нас, мы увидим оперение - крестик.

Символически векторное произведение можно записать двумя способам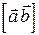и: или 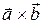(иногда векторы разделяют запятыми )

.

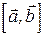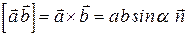Только квадратные скобки и ни какие другие. Из рис. 6 видно, что модуль векторного произведения имеет простой геометрический смысл - выражение absina численно равно площади параллелограмма, построенного на перемножаемых векторах. Если векторы параллельны a =0, sina = 0, .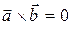

Поскольку направление вектора - результата векторного произведения определяется направлением вращения от первого сомножителя ко второму, результат векторного перемножения зависит от порядка сомножителей. Перестановка сомножителей вызывает изменение направления результирующего вектора на противоположное.

.

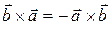Для вычисления удобно представить векторное произведение в виде определителя:

,

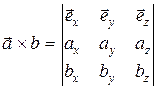где 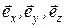- орты координатных осей, a_x, a_y, a_z, b_х, b_y, b_z - проекции векторов 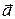и 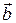на соответствующие оси. Тогда

.

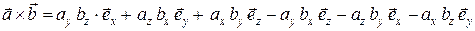Группируя одинаково направленные векторы, получаем

.

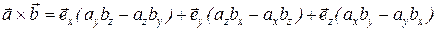8. Смешанное произведение.

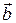Смешанным (или скалярно - векторным) произведением трех векторов называется выражение , то есть скалярное произведение вектора на векторное произведение векторов и 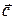. Согласно определениям скалярного и векторного произведений

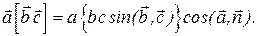
Здесь 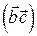- угол между 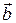и 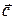, 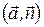- угол между и ортом 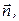определяющим направление вектора 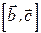. Из рис. 1.7 видно, что выражение 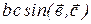численно равно площади основания параллелепипеда, построенного на перемножаемых векторах, а выражение 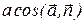численно равно высоте этого параллелепипеда, взятой со знаком “+”, если угол 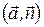острый, и со знаком “-”, если этот угол тупой. Следовательно, выражение имеет простой геометрический смысл - оно численно равно объему параллелепипеда, построенного на перемножаемых векторах (взятому со знаком “+” или “ -“ в зависимости от величины угла 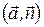). При вычислении объема параллелепипеда результат не может зависеть от того, какая из его граней взята в качестве основания. Отсюда следует, что

Таким образом, смешанное произведение допускает циклическую перестановку сомножителей, т. е. замену каждого из сомножителей следующим за ним в цикле:

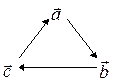
9. Производная вектора.

Рассмотрим вектор, который изменяется со временем по известному закону 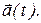Проекции этого вектора на координатные оси представляют собой заданные функции времени. Следовательно,

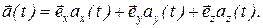
Мы предполагаем, что координатные оси не поворачиваются в пространстве, так что орты осей со временем не изменяются.

Тогда производная (скорость изменения) этой векторной функции по времени будет определяться следующим образом:

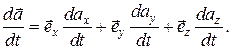
Это означает, что проекции вектора 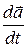на координатные оси равны производным по времени проекции вектора .

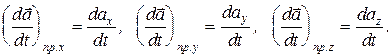
Производная произведения функции. Рассмотрим функцию , которая равна произведению скалярной функции j(t) на векторную функцию 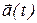: 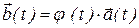или сокращено: 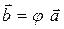. Производная 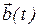по времени будет равна:

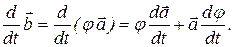
Производная скалярного произведения двух векторных функций времен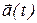и и определяется

.

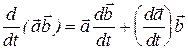Два квадрата векторной функции 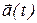имеем

.

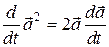Наконец, для векторного произведения производная определяется как:

.

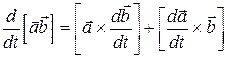Дата добавления: 2014-01-11