
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Векторная величина
|
|
|
|
vср =  (2.4)
(2.4)
называется средней скоростью движения материальной точки. По направлению вектор средней скорости совпадает с вектором перемещения (рис. 2.3). Уравнение (2.4.) позволяет определить единицу измерения скорости. В системе СИ единица скорости - м/с.
Но эта величина не полностью характеризует движение точки, так как из точки А в точку В материальная точка может перемещаться по разным траекториям, проходя при этом за один и тот же промежуток времени разной величины путь DS (рис.2.3.). Путь DS – величина скалярная. При криволинейном движении DS >  , для прямолинейного движения DS =
, для прямолинейного движения DS =  .
.
Если необходимо знать, с какой скоростью тело двигалось по той или иной траектории, то используется понятие среднего модуля скорости, который определяется отношением пути к промежутку времени, за который пройден этот путь.
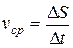 (2.5.)
(2.5.)
Средний модуль скорости — это скалярная величина, она не учитывает направление движения.
Более общей характеристикой движения материальной точки является мгновенная скорость, величина которой получается, если взять предел отношения
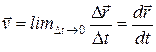 . (2.6)
. (2.6)
Мгновенная скорость – это предельное значение, к которому стремится вектор средней скорости при стремлении интервала времени  к нулю. Мгновенная скорость характеризует скорость тела в данной точке в данный момент времени, направлена всегда по касательной к траектории движения (рис. 2.3)
к нулю. Мгновенная скорость характеризует скорость тела в данной точке в данный момент времени, направлена всегда по касательной к траектории движения (рис. 2.3)
При  , стремящемся к нулю, модуль перемещения |
, стремящемся к нулю, модуль перемещения | r | будет мало отличаться от длины участка траектории, пройденного телом за этот промежуток времени, т. е. можно считать, что численное значение мгновенной скорости совпадает со значением среднего модуля скорости.
r | будет мало отличаться от длины участка траектории, пройденного телом за этот промежуток времени, т. е. можно считать, что численное значение мгновенной скорости совпадает со значением среднего модуля скорости.
 (2.7)
(2.7)
Пример1. Тело, двигаясь на плоскости с постоянной по величине скоростью, за время t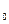 описывает траекторию, равную половине окружности радиуса R (рис. 2.4). Определить перемещение и вектор средней скорости тела за это время. Как отличается средняя скорость от мгновенной скорости?
описывает траекторию, равную половине окружности радиуса R (рис. 2.4). Определить перемещение и вектор средней скорости тела за это время. Как отличается средняя скорость от мгновенной скорости?
Пусть r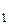 и r
и r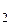 . — радиус-векторы, проведенные в начало и конец траектории. По определению перемещением является вектор АВ. При этом АВ=
. — радиус-векторы, проведенные в начало и конец траектории. По определению перемещением является вектор АВ. При этом АВ=  r = r
r = r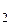 - r
- r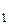 . Модуль перемещения |
. Модуль перемещения | r =2R.
r =2R.
Вектор средней скорости 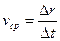 совпадает по направлению с отрезком АВ и равен по величине
совпадает по направлению с отрезком АВ и равен по величине 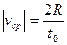 .
.
Мгновенная скорость в каждый момент времени направлена по касательной к траектории (окружности) и равна численно среднему модулю скорости:
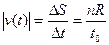 (2.8)
(2.8)
 | |||||
Рис.2.4.
Если траектория движения тела – прямая линия, то такое движение называют прямолинейным, а если скорость тела постоянна, то его называют еще и равномерным. Равномерным прямолинейным движением будем называть такое движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения.
Рассмотрим равномерное прямолинейное движение вдоль какой-либо оси ОХ. Предположим, движение точки начинается с момента времени 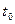 =0, причем в этот момент времени его координата (начальная координата) равна
=0, причем в этот момент времени его координата (начальная координата) равна  . Если координату тела в любой момент времени обозначить x(t), то зависимость координаты от времени имеет вид:
. Если координату тела в любой момент времени обозначить x(t), то зависимость координаты от времени имеет вид:
 (2.9)
(2.9)
Если точка движется в пространстве, то ее положение можно описать и с помощью радиуса-вектора:
r(t)= (2.10)
(2.10)
Пример 2. Одновременно из городов А и В, расстояние между которыми s =300 км, навстречу друг другу выезжают две автомашины со скоростями 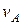 = 60 км/ч и
= 60 км/ч и 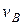 =40 км/ч. Определить место и время встречи машин.
=40 км/ч. Определить место и время встречи машин.
 |
Рис.2.5.
Решим задачу графически и аналитически. Поместим начало координат в точке А. Ось OX направим по направлению движения машины (рис. 2.5), выехавшей из пункта А. Тогда график движения для автомашин, выехавших из пунктов А и В, изобразится линиями I и П. Точка пересечения линий определяет координату и время встречи. Таким образом, 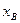 =180 км, t =3 ч.
=180 км, t =3 ч.
Для аналитического решения задачи запишем кинематический закон движения для обеих машин:
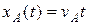 (2.11)
(2.11)
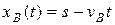
В момент встречи их координаты совпадают, т. е. 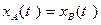 или
или 
Отсюда:
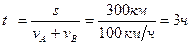 (2.12)
(2.12)

Пример 3. Человек в лодке переплывает реку, отправляясь из точки А (рис. 2.6). Если он направит лодку перпендикулярно берегу, то через время 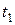 после начала движения он попадает в точку С, находящуюся на расстоянии s ниже точки В по течению реки. Если он направит скорость лодки под некоторым углом
после начала движения он попадает в точку С, находящуюся на расстоянии s ниже точки В по течению реки. Если он направит скорость лодки под некоторым углом  к перпендикуляру АВ, то попадает в точку В через время
к перпендикуляру АВ, то попадает в точку В через время  .
.
Определить ширину реки l, скорость лодки u относительно воды, скорость течения реки  и угол
и угол  , под которым лодочник направил лодку во втором случае.
, под которым лодочник направил лодку во втором случае.
В этой задаче имеет место случай двумерного движения тела, т. е. положение тела в любой момент времени необходимо задавать с помощью двух координат х и у.
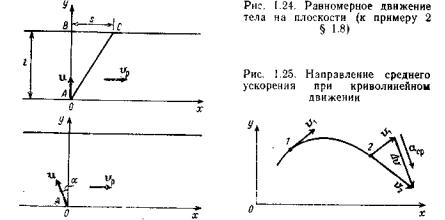
| Рис.2.6. | Рис.2.7. |
Выберем систему координат XOY, как показано на рис. 2.6, и запишем закон движения лодок для двух случаев вдоль осей OX и OY.
В первом случае:
 (2.13)
(2.13)

Для момента времени 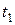 эти уравнения примут вид:
эти уравнения примут вид:
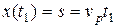 (2.14)
(2.14)
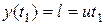
Во втором случае для любого момента времени t
 (2.15)
(2.15)
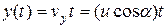
Для момента времени  эти уравнения запишутся:
эти уравнения запишутся:
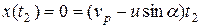 (2.16)
(2.16)
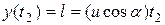 (2.17)
(2.17)
Таким образом, имеется система из четырех уравнений (1.25,26,27,28), которая позволит определить все неизвестные в задаче величины. Скорость течения реки определяется из уравнения (1.25). Угол  можно определить из уравнений (1.25) и (1.28):
можно определить из уравнений (1.25) и (1.28):
 (2.18)
(2.18)
Скорость лодки определяется из уравнения (1.27):
 (2.19)
(2.19)
Ширину реки можно определить из уравнения (1.25) или (1.28):
 (2.20)
(2.20)
3. СРЕДНЕЕ И МГНОВЕННОЕ УСКОРЕНИЕ.
В случае неравномерного движения необходимо знать, как быстро изменяется скорость с течением времени. Для характеристики быстроты изменения скорости движущейся точки вводится новая физическая величина, называемая ускорением. По аналогии со скоростью вводят понятие среднего ускорения. Среднее ускорение — это векторная величина, равная отношению вектора изменения (приращения) скорости  v к интервалу времени, за который происходит это изменение:
v к интервалу времени, за который происходит это изменение:
а  (3.1)
(3.1)
Этот вектор направлен в ту же сторону, что и  v.
v.
Среднее ускорение недостаточно точно описывает процесс изменения скорости. Важно знать изменение скорости в каждый момент времени. В связи с этим вводят понятие мгновенного ускорения — мгновенное ускорение определяется предельным отношением вектора изменения скорости к интервалу времени, за который произошло изменение при стремлении этого интервала к нулю, т. е.
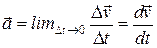 (3.2)
(3.2)
При заданной траектории движения легко определить направление скорости в каждой точке траектории, которое совпадает с направлением касательной в этой точке, однако при заданном направлении скорости вектор ускорения
может иметь любое направление. Оно определяется изменением скорости 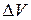 за бесконечно малый интервал времени вблизи той точки, которая нас интересует.
за бесконечно малый интервал времени вблизи той точки, которая нас интересует.
Проекции вектора ускорения на оси координат отражают быстроту изменения скорости вдоль этих осей и определяются аналогичным образом:
А , а
, а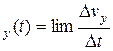 , а
, а . (3.3)
. (3.3)
Формула (1.33) позволяет легко установить единицу измерения ускорения. В системе СИ единица ускорения равна
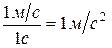 (3.4)
(3.4)
Если скорость тела возрастает с течением времени, то движение называется ускоренным, если скорость тела уменьшается со временем — замедленным. В дальнейшем мы будем рассматривать только движение с постоянным ускорением. В этом случае значение среднего ускорения совпадает со значением мгновенного ускорения.
Рассмотрим прямолинейное движение точки вдоль оси ОХ с постоянным ускорением а 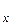 с момента времени
с момента времени  =0, когда скорость ее достигла уже некоторого значения
=0, когда скорость ее достигла уже некоторого значения  . Скорость при таком равноускоренном движении равна:
. Скорость при таком равноускоренном движении равна:
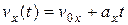 . (3.5)
. (3.5)
Для вектора скорости:
v (t) = v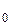 +a t (3.6)
+a t (3.6)
Закон движения (зависимость координаты точки от времени) при равноускоренном движении имеет вид:
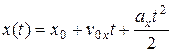 (3.7)
(3.7)
Для трехмерного движения положение точки в любой момент времени при равноускоренном движении можно определить и с помощью радиуса-вектора:
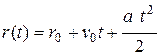 (3.8)
(3.8)
4. НОРМАЛЬНАЯ И ТАНГЕНЦИАЛЬНАЯ СОСТАВЛЯЮЩИЕ УСКОРЕНИЯ.
Вектор ускорения, по определению, равен изменению вектора скорости точки за единицу времени. Но изменение любого вектора включает в себя изменение его численной величины (модуля) и изменение его направления. Поэтому при вычислении ускорения нужно знать обе его составляющие.
Пусть некоторая материальная точка движется по траектории, имеющей форму произвольной кривой (рис.41). В начальный момент времени она находилась в точке А, а через промежуток времени Dt - в точке В. При этом ее скорость изменилась от  до. Найдем изменение вектора скорости
до. Найдем изменение вектора скорости 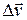 .
.
 Для этого перенесем вектор
Для этого перенесем вектор  параллельно самому себе в точку А. Тогда
параллельно самому себе в точку А. Тогда 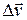 изобразится на чертеже вектором, соединяющим конец вектора
изобразится на чертеже вектором, соединяющим конец вектора  и конец вектора АD =
и конец вектора АD = .
.
Отложив на отрезке АD отрезок АК длиной АС (от точки А), найдем, что длина отрезка КD = 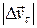 определит изменение модуля вектора скорости
определит изменение модуля вектора скорости  , а направлен вектор
, а направлен вектор  будет по направлению вектора скорости
будет по направлению вектора скорости  . Если теперь соединить конец вектора скорости
. Если теперь соединить конец вектора скорости  (точку С) с точкой К вектором
(точку С) с точкой К вектором 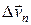 , то получим векторный треугольник СКD, в котором
, то получим векторный треугольник СКD, в котором 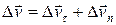 .
.
Ускорение  рассматриваемой материальной точки, по определению, равно:
рассматриваемой материальной точки, по определению, равно:
 . (3.1)
. (3.1)
Здесь  - составляющая вектора полного ускорения, определяющая изменение численного значения скорости, а
- составляющая вектора полного ускорения, определяющая изменение численного значения скорости, а  - составляющая вектора полного ускорения, определяющая изменение направления вектора скорости.
- составляющая вектора полного ускорения, определяющая изменение направления вектора скорости.
В пределе (Dt®0) точка В неограниченно приближается к точке А, направление вектора  стремится к направлению вектора
стремится к направлению вектора  , следовательно, и вектор
, следовательно, и вектор  стремится к направлению вектора
стремится к направлению вектора  , а это значит, что и вектор
, а это значит, что и вектор  стремится к направлению вектора
стремится к направлению вектора  . Эту составляющую полного ускорения поэтому называют касательной, или тангенциальной, составляющей:
. Эту составляющую полного ускорения поэтому называют касательной, или тангенциальной, составляющей:
 (4.2)
(4.2)
При условии Dt®0 кривая АВ совпадает с другой окружности некоторого радиуса R и центром в точке 0. R называется радиусом кривизны траектории, а точка O - центром кривизны для данной точки кривой.
Если в точках А и В провести радиусы кривизны кривой, то они будут перпендикулярны векторам 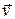 и
и  , так как вектор скорости всегда направлен по касательной к траектории. Угол ÐАОВ= Da между радиусами в пределе Dt®0 тоже стремиться к нулю. Из рис.11 видно, что Ð КАС тоже равен Da.
, так как вектор скорости всегда направлен по касательной к траектории. Угол ÐАОВ= Da между радиусами в пределе Dt®0 тоже стремиться к нулю. Из рис.11 видно, что Ð КАС тоже равен Da.
При условии Da®0 из DСАК можно получить 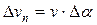 . Учитывая это, получим:
. Учитывая это, получим:
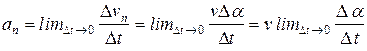 . (4.3)
. (4.3)
Пройденный путь между точками А и В DS при условии Dt ®0 является другой окружности радиуса R и определяется DS = R Da.
Умножим и разделим выражение для an на R. Получим:
 . (4.4)
. (4.4)
По определению скорости
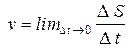 . (4.5)
. (4.5)
Тогда
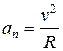 . (4.6)
. (4.6)
Численное значение нормального ускорения прямо пропорционально квадрату скорости движения материальной точки и обратно пропорционально радиусу кривизны траектории движения частицы в данной точке. Так как в пределе Dt®0 вектор  стремится по направлению к вектору
стремится по направлению к вектору  , то вектор
, то вектор 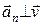 стремится по направлению к АО, т. е. будет направлен по радиусу кривизны к центру кривизны траекторий. Поэтому эту составляющую полного ускорения называют центростремительным, или нормальным (от слова “нормаль”), ускорением.
стремится по направлению к АО, т. е. будет направлен по радиусу кривизны к центру кривизны траекторий. Поэтому эту составляющую полного ускорения называют центростремительным, или нормальным (от слова “нормаль”), ускорением.
Подводя итог всем этим рассуждениям, можно сформулировать следующее утверждение: любое криволинейное движение - движение с ускорением.
|
|
|
|
|
Дата добавления: 2014-01-11; Просмотров: 1052; Нарушение авторских прав?; Мы поможем в написании вашей работы!