Пример. 1) В прокатном стане на входе такого потока есть стальные заготовки сечением 200х200 мм, а на выходе – стальная лента толщиной 1 мм

1) В прокатном стане на входе такого потока есть стальные заготовки сечением 200х200 мм, а на выходе – стальная лента толщиной 1 мм, шириной 2 метра.

2) В гидроэлектростанции на входе – поток воды с напором 20 м и расходом 150 м³/с, а на выходе – электрический ток напряжением 380 В и частотой 50 Гц.

§6.1.3. Функциональная структура

Подавляющее большинство ТО состоит из нескольких элементов (агрегатов, блоков, узлов). Элементы ТО взаимосвязаны и взаимодействуют. Поскольку каждый элемент как самостоятельный ТО выполняет определённую функцию и реализует определённую ФО, то между элементами имеют место два вида связей.

Во-первых, это функциональные связи, посредством которых элементы образуют конструктивную функциональную структуру. Конструктивная ФС представляет собой орграф, вершинами которого являются наименования элементов, а дугами – функции элементов. Методика построения конструктивных ФС будет описана в §6.5.

Во-вторых, кроме функциональных связей между элементами ТО существуют ещё потоковые связи: элементы, реализуя определённые физические операции, образуют поток преобразуемых веществ, энергии, сигналов или других факторов.

Такие потоки определённым образом объединяют и связывают элементы ТО и их ФО. Взаимосвязанный набор физических операций, реализующих один определённый поток преобразований вещества, энергии или сигналов, называется потоковой ФС. Потоковая ФС представляет собой орграф, вершинами которого являются наименования элементов ТО или наименования операций Коллера, а дугами – входные и выходные потоки (факторы). Если в вершинах графа указаны наименования элементов ТО, то такая ФС называется конкретизированной потоковой ФС. Если в вершинах графа указаны наименования операций Коллера, то такая ФС называется абстрагированной потоковой ФС или структурой физических операций.

§6.1.4. Физический принцип действия

В потоковой ФС каждый элемент реализует определённую ФО. Такая реализация происходит на основе одного или нескольких физико-технических эффектов.

Под физико-техническим эффектом будем понимать различные приложения физических законов, физические явления, которые могут быть реализованы в технических устройствах.

Наиболее обобщённое описание ФТЭ – это тройка

(А,В,С), где

А – входной поток вещества, энергии или сигналов;

С - выходной поток вещества, энергии или сигналов;

В – физический объект, обеспечивающий преобразование А в С.

Примеры ФТЭ приведены в таблице.

Наименование ФТЭ	А	В	С
Закон Гука	Сила	Твёрдое тело	Линейная деформация
Закон Джоуля – Ленца	Электрический ток	Проводник	Теплота
Пьезоэлектрический эффект	Деформация	Пьезокристалл	Электрическое поле

Элементарная физическая операция - это такая ФО, которая может быть реализована с помощью только одного ФТЭ. Как правило, физические операции состоят из нескольких последовательно соединённых ФТЭ.

Под физическим принципом действия (ФПД) понимается орграф, вершинами которого являются наименования физических объектов В, а дугами – входные и выходные потоки вещества, энергии или сигналов. Таким образом, физический принцип действия – это физическая операция, представленная в виде цепочки связанных ФТЭ.

Описание ФПД содержит изображение принципиальной схемы ТО, в которой в упрощённом виде показаны основные конструктивные элементы, обеспечивающие реализацию ФПД.

§6.1.4. Техническое решение и проект

Техническое решение (ТР) представляет собой конструктивное оформление ФПД. ТР содержит следующие признаки технического объекта:

- перечень основных элементов;

- взаимное расположение элементов в пространстве;

- связи элементов (способы и средства соединения);

- последовательность взаимодействия элементов во времени;

- особенности конструктивного исполнения элементов (форма, материал и т.д.);

- принципиально важные соотношения параметров.

Техническое решение конкретного ТО может быть описано с любой степенью детализации, и.е. сначала описывают ТР устройства в целом, затем ТР каждого блока, затем – каждого узла и т.д. Описание ТР на естественном языке, как правило, дополняется его графическим изображением (например, эскизом).

ТР представляет собой как бы безразмерное описание ТО, которое может иметь большое число реализаций по параметрам. Параметры – это размеры ТО и его элементов, количественные характеристики входных и выходных потоков и другие измеряемые свойства ТО.

В отличие от ТР в проекте указываются значения параметров ТО и всех его элементов до деталей. Он содержит всю необходимую информацию для изготовления и эксплуатации ТО. Проект – это рабочие чертежи и конструкторская документация.

§6.2. Задачи поиска и выбора проектно-конструкторских решений

При разработке любого ТО конструктору предстоит решить последовательность задач выбора проектно-конструкторских решений. Эта последовательность имеет свою иерархию, полностью соответствующую иерархии описаний ТО.

Рассмотрим эти задачи.

1. Составление или уточнение описания потребности (функции). Здесь наряду с качественным описанием указывают основные количественные характеристики действия D, объекта G, условий и ограничений H.

2. Выбор физической операции. Чаще всего для реализации одной и той же потребности существует несколько альтернативных ФО. Проектировщику предстоит выбрать наиболее перспективную из них.

3. Выбор функциональной структуры. Для реализации одной и той же технической функции возможно построение нескольких альтернативных функциональных структур, из которых также предстоит выбрать наиболее рациональную.

4. Выбор физического принципа действия. У одной и той же потоковой ФС различные элементы могут быть реализованы на основе различных физико-технических эффектов. Следовательно, может быть синтезировано большое число возможных ФПД, из которых надо выбрать наиболее перспективный вариант.

5. Выбор технического решения. Один и тот же ФПД может быть реализован несколькими, а иногда очень большим числом (сотни и тысячи) практически приемлемых вариантов ТР, из которых выбирают лучший.

6. Выбор параметров ТО. При решении этой задачи ставят и решают иерархическую последовательность подзадач поиска и выбора оптимальных параметров ТО и его элементов.

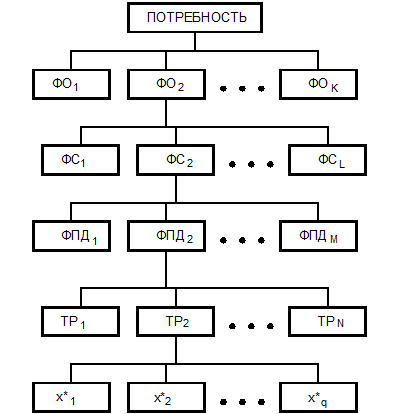
1 уровень

2 уровень

3 уровень

4 уровень

5 уровень

6 уровень

Хотя все эти типы задач можно отнести к творческим инженерным задачам, наиболее творческими являются задачи уровней 2 – 4. Приведённая схема идеализирована, реально проектирование и конструирование идёт итерационно, со многими возвратами.

Заметим, что с повышением уровня задачи(от 6 к 1) её успешное решение даёт больший экономический эффект. Так, решение задачи 6 уровня улучшает технико-экономические показатели на 10–15%, 5 уровня – на 20-30%, 4 уровня – на 30-50%.

Ещё более важным оказываются изобретения и обоснования новых потребностей и ФО.

4.7.3. Сравнение вариантов. Постановка задачи оптимизации.

Варьируемые параметры, критерий выбора, целевая функция.

Операцией называется всякое мероприятие (система действий), объединенное единым замыслом и направленное к достижению определённой цели. В случае морфологического анализа операция – это выбор наилучшей конструкции.

Операция есть всегда управляемое мероприятие, т. е. от нас зависит, каким способом выбрать некоторые параметры, характеризующие её организацию. «Организация» здесь понимается в широком смысле слова, включая набор технических средств, применяемых в операции.

Всякий определенный выбор зависящих от нас параметров называется решением.

Те параметры, совокупность которых образует решение, называются элементами решения. В качестве элементов решения могут фигурировать различные числа, векторы, функции, физические признаки и т. д.

В случае морфологической таблицы элементами решения будут номера вариантов исполнения признаков.

Совокупность пар чисел x.y (где x – номер признака, а y – номер варианта исполнения этого признака) образует решение.

Для упрощения мы будем всю совокупность элементов решения обозначать одной буквой х и говорить «решение х».

Чтобы сравнивать между собой по эффективности разные решения, нужно иметь какой-то количественный критерий, так называемый показатель эффективности W (его часто называют «целевой функцией»). Этот показатель выбирается так, чтобы он отражал целевую направленность операции. «Лучшим» будет считаться то решение, которое в максимальной степени способствует достижению поставленной цели. Чтобы выбрать, «назвать по имени» показатель эффективности W, нужно прежде всего спросить себя: чего мы хотим, к чему стремимся, предпринимая операцию? Выбирая решение, мы, естественно, предпочтем такое, которое обращает показатель эффективности W в максимум (или в минимум). Например, доход от операции хотелось бы обратить в максимум; если же показателем эффективности являются затраты, их желательно обратить в минимум. Если показатель эффективности желательно максимизировать, мы это будем записывать в виде W Þ max, а если минимизировать — W ® min.

Прямые и обратные задачи исследования операций

Задачи исследования операций делятся на две категории: прямые и обратные.

Прямые задачи отвечают на вопрос: «Что будет, если...?» Что будет, если в заданных условиях мы примем некоторое решение х Î X? В частности, чему будет равен, при данном решении х, выбранный показатель эффективности W? Для решения такой задачи строится математическая модель, позволяющая выразить один или несколько показателей эффективности через заданные условия и элементы решения.

Обратные задачи отвечают на вопрос: «Как сделать, чтобы…?» Как выбрать решение х для того, чтобы показатель эффективности W обратился в максимум?

Очевидно, что прямые задачи проще обратных и что для решения обратной задачи прежде всего надо уметь решать прямую.

Для некоторых типов операций прямая задача решается настолько просто, что ею специально не занимаются. Для других типов операций построение математических моделей и вычисление показателя эффективности само по себе далеко не тривиально.

Остановимся несколько подробнее на обратных задачах. Если число возможных вариантов решения, образующих множество X, невелико, то можно попросту вычислить величину W для каждого из них, сравнить между собой полученные значения и непосредственно указать один или несколько оптимальных вариантов, для которых W достигает максимума. Такой способ нахождения оптимального решения называется «простым перебором». Однако, когда число возможных вариантов решения, образующих множество X, велико, поиск среди них оптимального «вслепую», простым перебором, затруднителен, а зачастую практически невозможен. В этих случаях применяются методы «направленного перебора», обладающие той общей особенностью, что оптимальное решение находится рядом последовательных «попыток» или «приближений», из которых каждое последующее приближает нас к искомому оптимальному.

Постановка задачи оптимизации (обратной задачи ИСО) в общей форме

Пусть есть некоторая операция 0, на успех которой мы можем влиять, выбирая тем или другим способом решение х (вспомним, что х — не число, а целая группа параметров). Пусть эффективность операции характеризуется одним показателем W ® max.

Пусть все условия операции полностью известны заранее, не содержат неопределенности. Тогда все факторы, от которых зависит успех операции, - это зависящие от нас элементы решения, образующие в своей совокупности решение х.

Показатель эффективности W зависит от факторов. Это мы запишем в виде формулы:

W=W(,x) (1)

Будем считать, что вид зависимости (1) нам известен, т. е. прямая задача решена. Тогда обратная задача формулируется следующим образом:

Найти такое решение х = х*, которое обращает показатель эффективности W в экстремум, например, в максимум.

W* = max {W (х)}. (2)

xÎX

Формула (2) читается так: W* есть максимальное значение W(a, х), взятое по всем решениям, входящим в множество возможных решений X.

Итак, перед нами — типичная математическая задача нахождения максимума функции или функционала.

Эта задача принадлежит к классу так называемых «вариационных задач». Самые простые из таких задач - «задачи на максимум и минимум». Чтобы найти экстремум функции многих аргументов, надо продифференцировать ее по всем аргументам (в данном случае — элементам решения), приравнять производные нулю и решить полученную систему уравнений. Но эта задача не так проста, как кажется на первый взгляд. Во-первых, систем уравнений (элементов решения) может быть много. Во-вторых, когда на элементы решения наложены ограничения, экстремум часто достигается не в точке, где производные равны нулю (такой точки может вообще не быть), а где-то на границе области X- очень сложная т.н. «многомерная вариационная задача при ограничениях». В-третьих, функция W может вообще не иметь производных (например, задана только для целочисленных значений аргументов).

Все это делает задачу поиска экстремума далеко не такой простой, как она кажется с первого взгляда.

Существует целый набор численных методов отыскания экстремумов, некоторые из них включают элемент «случайного поиска», который для многомерных задач нередко оказывается эффективнее упорядоченного перебора.

Таким образом, задача нахождения оптимального решения в простейшем, детерминированном случае есть чисто математическая задача, принадлежащая к классу вариационных (при отсутствии или наличии ограничений), которая может представить вычислительные, но не принципиальные трудности.

4.7.4. Многокритериальная оптимизация.

До сих пор рассматривались только самые простые случаи, когда ясен критерий, по которому производится оценка эффективности, и требуется обратить в максимум (минимум) один-единственный показатель W. К сожалению, на практике такие задачи, где единственный критерий оценки однозначно диктуется целевой направленностью операции, встречаются не так уж часто — преимущественно при рассмотрении небольших по масштабу и скромных по значению мероприятий. А когда идет речь о крупномасштабных, сложных операциях, затрагивающих разнообразные интересы их организаторов и общества в целом, то их эффективность, как правило, не может быть полностью охарактеризована с помощью одного-единственного показателя эффективности W. На помощь ему приходится привлекать другие, дополнительные. Такие задачи исследования операций называются многокритериальными.

Рассмотрим пример такой задачи. Организуется оборона важного объекта от воздушных налетов. В нашем распоряжении — какие-то средства противовоздушной обороны, которые надо разумным образом разместить вокруг объекта, организовать их взаимодействие, распределить между ними цели, назначить боезапас и т. д. Допустим, что каждый из самолетов противника, участвующих в налете, является потенциальным носителем мощного поражающего средства, которое, будучи применено по объекту, гарантирует его уничтожение. Тогда главная задача операции — не допустить к объекту ни одного самолета, а естественный показатель эффективности — вероятность W того, что ни один самолет не прорвется к объекту. Но единственный ли это важный для нас показатель? Безусловно, нет. При одной и той же вероятности W мы предпочтем все-таки решение, при котором будет погибать в среднем побольше самолетов противника. Отсюда второй показатель эффективности М — среднее число пораженных целей, который нам тоже хотелось бы максимизировать. Кроме того, нам далеко не все равно, каковы будут наши собственные боевые потери П — еще один критерий, который хотелось бы минимизировать. Желательно было бы, кроме того, сделать поменьше средний расход боеприпасов R, и т. д.

Другой пример — на этот раз из совершенно мирной области. Организуется (или реорганизуется) работа промышленного предприятия. Под углом зрения какого критерия надо выбирать решение? С одной стороны, нам хотелось бы обратить в максимум валовой объем продукции V. Желательно также было бы получить максимальный чистый доход D. Что касается себестоимости S, то ее хотелось бы обратить в минимум, а производительность труда П — в максимум. При обдумывании задачи может возникнуть еще ряд дополнительных критериев.

Такая множественность показателей эффективности, из которых одни желательно обратить в максимум а другие — в минимум, характерна для любой сколько-нибудь сложной задачи исследования операций.

Итак, типичной для крупномасштабной задачи исследования операций является многокритериальность — наличие ряда количественных показателей W₁, W₂..., одни из которых желательно обратить в максимум, другие — в минимум.

Спрашивается, можно ли найти решение, одновременно удовлетворяющее всем этим требованиям? Со всей откровенностью ответим: нет. Решение, обращающее в максимум один какой-то показатель, как правило, не обращает ни в максимум, ни в минимум другие.

Как же решаются такие задачи? Возможно, есть способы сведения многокритериальных задач к однокритериальным? Да, такие способы есть, хотя их использование привносит в задачи значительную субъективность.

1) Нередко применяется следующий способ составления «обобщенного показателя эффективности». Он представляет собой «взвешенную сумму» частных показателей, в которую каждый из них W_i, входит с каким-то «весом» d_i, отражающим его важность:

W = d₁ W₁ + d₂ W₂ +... (1)

Для тех показателей, которые желательно увеличить, веса берутся положительными, уменьшить — отрицательными.

При произвольном назначении весов d_i этот способ не приводит к сколько-нибудь достоверным результатам. Но если оценку весовым коэффициентам даёт опытный эксперт (а лучше, группа экспертов), и их независимые оценки усредняются, то можно говорить об определённой приближённости модели к реальности.

2) Существует ещё один, часто применяемый способ свести многокритериальную задачу к однокритериальной — это выделить один (главный) показатель W_ГЛ и стремиться его обратить в максимум, а на все остальные W₁, W₂, … наложить только некоторые ограничения, потребовав, чтобы они были не меньше (или не больше) каких-то заданных величин. Например, при оптимизации плана работы предприятия можно потребовать, чтобы прибыль была максимальна, план по ассортименту — выполнен или перевыполнен, а себестоимость продукции — не выше заданной. При таком подходе все показатели, кроме одного — главного, переводятся в разряд заданных условий a.

Существуют способы осмыслить решение многокритериальных задач, не прибегая к свёртке или замене критериев.

3) Математический аппарат не панацея, и не следует слепо доверять рекомендациям математических выкладок. Но он помогает «выбраковать» из множества возможных решений Х заведомо неудачные, уступающие другим по всем критериям.

Покажем, как это делается. Пусть имеется многокритериальная задача исследования операций с k критериями W₁, W₂,..., W_К. Для простоты предположим, что все эти величины желательно максимизировать (как переходить от «минимума» к «максимуму», мы уже знаем). Пусть в составе множества возможных решений есть два решения х₁ и х₂ такие, что все критерии W₁, W₂,..., W_К для первого решения больше или равны соответствующим критериям для второго решения, причем хотя бы один из них действительно больше. Очевидно, тогда в составе множества Х нет смысла сохранять решение х₂, оно вытесняется (или, как говорят, «доминируется») решением х₁. Ладно, выбросим решение x₂ как неконкурентоспособное и перейдем к сравнению других решений по всем критериям. В результате такой процедуры отбрасывания заведомо непригодных, невыгодных решений множество Х обычно сильно уменьшается: в нем сохраняются только так называемые эффективные (иначе «паретовские») решения, характерные тем, что ни для одного из них не существует доминирующего решения.

Проиллюстрируем прием выделения паретовских решений на примере задачи с двумя критериями: W₁ и W₂ (оба требуется максимизировать). Множество Х состоит из конечного числа n возможных решений х₁, x₂, … x_n. Каждому решению соответствуют определенные значения показателей W₁, W₂. Будем изображать решение точкой на плоскости с координатами W₁, W₂ и занумеруем точки соответственно номеру решения (рис). Очевидно, из всего множества А эффективными будут только решения х₆, x₇, x₈, x₉, лежащие на правой верхней границе области возможных решений (см. жирные точки, соединенные пунктиром, на рис). Для всякого другого решения существует хотя бы одно доминирующее, для которого либо W₁, либо W₂, либо оба больше, чем для данного. И только для решений, лежащих на правой верхней границе, доминирующих не существует.

Когда из множества возможных решений выделены эффективные, «переговоры» могут вестись уже в пределах этого «эффективного» множества. На рис. его образуют четыре решения: х₆, x₇, x₈, x₉, из них х₆ —наилучшее по критерию W₁, x₉ — по критерию W₂. Дело лица, принимающего решение, выбрать тот вариант, который для него предпочтителен и «приемлем» по обоим критериям.

Аналогично строится множество эффективных решений и в случае, когда показателей не два, а больше (при числе их, большем трех, геометрическая интерпретация теряет наглядность, но суть дела сохраняется). Множество эффективных решений легче обозримо, чем полное множество X. Что касается окончательного выбора решения, то он по-прежнему остается прерогативой человека. Только человек, с его непревзойденным умением решать неформальные задачи, принимать так называемые «компромиссные решения» (не строго оптимальные, но приемлемые по ряду критериев) может взять на себя ответственность за окончательный выбор.

§6.3. Структурная и параметрическая оптимизация

Параметрическая оптимизация. Есть список параметров, описывающих одно техническое решение для данного технического объекта: x₁, x₂, …x_i, …x_p.

Каждая их этих переменных может принимать ряд значений в своём диапазоне.

Решением называется набор чисел x²₁, x²₂, …x²_i, …x²_p,

где x²_i - некоторое допустимое значение параметра x_i.

Если хотя бы несколько параметров могут принимать больше, чем одно решение, то количество решений будет большим (в пределе – бесконечным). Все вместе решения образуют область допустимых решений.

Возникает задача оптимизации – выбора наилучшего решения из области решений. Такую задачу можно решить только в рамках заданного показателя эффективности (минимум массы, максимум надёжности, максимум экономической эффективности и т.д., либо комплексный показатель эффективности).

Сформулировать задачу оптимизации – это значит

1. записать показатель эффективности в виде математического выражения через переменные x₁, x₂, …x_i, …x_p и устремить его к оптимуму.

2. записать ограничения, налагаемые на переменные, в виде математических уравнений.

Например, есть два параметра x₁, x₂, на которые мы можем влиять, изменять их значения. Целевая функция F = a x₁+b x₂ ® max

x₁, x₂ ³ 0

x₁<c

x₂<d

x₁ + x₂£ 2c

Переменные x₁, x₂ можно представить в виде координатных осей. Ограничения, налагаемые на параметры, можно изобразить на этой плоскости. Если задача сформулирована правильно, то получится замкнутая область, и любая точка этой области будет решением, т.к. она имеет координаты (x²₁, x²₂).

В случае большего числа параметров постановка задачи остаётся такой же, но от плоскости мы переходим в многомерное пространство.

Перебирая точки области, можно найти такую точку (x*₁, x*₂, …x*_i, …x*_p), в которой показатель эффективности обращается в оптимум. Задача параметрической оптимизации решена.

Существует большое количество математических методов, применимых для параметрической оптимизации.

Структурная оптимизация.

Если есть два или больше технических решений, каждое из них описывается набором своих параметров. Например, имеем два технических решения ТР₁ и ТР₂. Они имеют различную структуру и описываются различными как по количеству, так и по составу параметрами.

ТР1: x₁, x₂, …x_i, …x_p.

ТР2: y₁, y₂, …y_j, …y_q.

Как их сравнить, чтобы выбрать лучшее?

Задавшись одним критерием сравнения, нужно решить задачу параметрической оптимизации для каждого ТР, а затем сравнить лучшие варианты между собой и выбрать лучшую структуру.

Существуют методы, применимые для структурной оптимизации, например, генетический алгоритм.

§6.4. Декомпозиция ТО.

§6.4.1. Принципы декомпозиции ТО.

В основу построения функциональной структуры положен принцип выделения и рассмотрения структур с двухуровневой иерархией: ТО разделяют на несколько элементов, каждый из которых имеет свою определённую функцию (или несколько функций) по обеспечению работы ТО. Сам технический объект представляет верхний уровень, а выделенные функциональные элементы – нижний.

При углублении анализа каждый выделенный элемент рассматривается как самостоятельный ТО, который также разделяется на несколько функциональных элементов и т.д. Объединение таких двухуровневых структур позволяет получить многоуровневую иерархическую структуру.

Главный момент в этом процессе – выделение двухуровневой структуры.

Предельное разделение ТО на элементы возможно до неделимых в функциональном смысле элементов (например, шарик в подшипнике).

Определение 1. Базовым (неделимым) элементом называется деталь (или часть детали) с минимальным числом функций по обеспечению работы других элементов системы, при любом делении которых появляются элементы, не имеющие самостоятельной функции или с одинаковыми функциями.

Одновременно с разделением ТО на элементы выделяют объекты окружающей среды, с которыми рассматриваемый ТО находится в функциональном или вынужденном взаимодействии и которые существенно влияют на конструкцию ТО. К таким объектам в первую очередь относят объекты, воспринимающие действие ТО (компонента G в описании потребности P=(D,G,H)). Также к таким объектам окружающей среды относятся подводимая энергия, управляющие сигналы, неблагоприятные излучения и другие воздействия, оказывающие существенное влияние на конструкцию ТО.

При декомпозиции ТО также большое внимание уделяется главным элементам.

Определение 2. К главным элементам относятся рабочие органы и другие элементы, которые непосредственно взаимодействуют с предметом обработки G и другими объектами окружающей среды.

Свойства главных элементов.

1. функция главного элемента совпадает с функцией ТО или в решающей мере зависит от последней;

2. объекты ОС для главного элемента, как правило, совпадают с объектами, на которые направлено действие ТО.

Пример.

ТО – ручка для письма, G – бумага, главный элемент – перо или шариковый узел. Функция главного элемента – образование на бумаге видимого следа – совпадает с функцией объекта.

§6.4.2. Описание функций элементов при декомпозиции ТО

При декомпозиции главным элементам приписывают имя Е₀₁, Е₀₂, и т. д. или Е₀, если он один. Остальным элементам присваивают имена Е₁, Е₂,… Е_n. Объекты окружающей среды, с которыми взаимодействуют ТО и его элементы, обозначаются через V₁, V₂, …

После того, как ТО разделён на элементы, необходимо описать функции этих элементов. Сами функции будем обозначать Ф₁, Ф₂,…, где индексы соответствуют обозначениям элементов. При описании функций элементов надо в скобках дублировать обозначения объектов окружающей среды и других элементов, которые участвуют в описании функции.

Результаты декомпозиции ТО на элементы и описание их функций оформляют в одной таблице анализа функций.

Приведём пример составления таблицы для ЖРД МТ. Сначала назовём объект и его функцию: ЖРД МТ – создаёт управляющий импульс силы для космического аппарата.

АНАЛИЗ ФУНКЦИЙ ЖРД МТ

Элемент	Функция
Обозн.	Наименование	Обозн.	Наименование
Е0	Камера	Ф0	Создаёт управляющий импульс силы для космического аппарата (V3)
Е1	Электромагнитный клапан «О»	Ф1	Управляет подачей р’ из трубопровода (V1) в камеру (Е0)
Е2	Электромагнитный клапан «Г»	Ф2	Управляет подачей р из трубопровода системы подачи топлива (V2) в камеру (Е0)
Е3	Сигнализатор давления	Ф3	Сигнализирует КА (V3) о работе камеры сгорания двигателя (Е0)

§6.5. Анализ и описание конструктивной функциональной структуры.

Конструктивная ФС представляет собой ориентированный граф, вершинами которого являются наименования элементов ТО и объектов ОС, а рёбрами – функции элементов.

Дата добавления: 2014-01-13