Порядок и правила построения конструктивной ФС

При построении ФС сначала изображают вершины графа. В первом по горизонтали ряду предпочтительнее располагать вершины – объекты ОС, а во втором – вершины – элементы ТО.

Направленные рёбра графа выходят из вершин – элементов и заканчиваются или в вершинах – элементах, работу которых они обеспечивают, или в вершинах – объектах ОС, взаимодействующих с рассматриваемыми элементами.

Из каждой вершины – элемента выходит столько рёбер, сколько функций выполняет элемент.

Вершины, в которых заканчиваются рёбра – функции, указаны в описании функций в скобках.

Конструктивные ФС имеют рёбра двух типов:

1 тип. Начинаются в одной вершине и заканчиваются в другой единственной вершине.

2 тип. Начинаются в одной вершине и через абстрактную И-вершину заканчиваются в 2х или более вершинах.

Рёбра 2-го типа описывают функции элементов, которые обеспечивают соединение или взаимодействие между другими несколькими элементами и объектами ОС. Всем рёбрам на графе присваиваются обозначения, совпадающие с обозначениями соответствующих функций элементов.

При изображении схемы надо постараться, чтобы число пересечений рёбер было минимальным. Допускается размещение элементов в 3-м ряду.

При изображении конструктивной ФС ЖПД МТ воспользуемся таблицей описания функций.

§6.6. Анализ и описание потоковой функциональной структуры.

Разделение ТО на элементы для потоковой ФС происходит аналогично декомпозиции ТО при построении конструктивной ФС. Однако при этом не выделяются главные элементы, а компоненты ОС обычно считают источниками входящих или оттоком выходящих потоков ВЭ|С. Объектам ОС присваивают номера О-1, О-2 и т.д.

Следует помнить, что элементы ТО могут представлять собой сложные агрегаты или узлы, для которых может быть построена своя потоковая ФС.

Описывать физическую операцию каждого выделенного элемента ТО надо в соответствии с формулой Q=(A_T,E,C_T).

Описание потоков должны включать:

А) наименование потока ВЭ|С;

Б) качественную характеристику потока, существенно влияющую на техническое решение ТО (например, для потока «электромагнитное излучение» качественная характеристика м/б «видимый свет»)

Описание ФО оформляют таблицей. Приведём пример такой таблицы для описания физической операции ЖРД МТ (см. таблицу 1).

Построение потоковой функциональной структуры

Как уже говорилось, конкретизированная потоковая ФС представляет собой орграф, вершинами которого являются наименования элементов, а рёбрами – входные и выходные потоки вещества, энергии или сигналов А_Т, С_Т.

В абстрагированной потоковой ФС вершинами графа являются не элементы, а операции Коллера Е.

Построим конкретизированную и абстрагированную потоковые ФС ЖРД МТ, воспользовавшись таблицей.

Таблица 1.

ФО ЖРД МТ: АТ – жидкое ракетное топливо Е - преобразование СЕ – управляющий импульс силы.
Элементы ТО и объекты ОС	Физическая операция
Номер	Наименование	АТ	N ист. ОС	Е	СТ	N приём.
О-1	Блок питания	-	-	-	Постоянное электрическое напряжение	1;2
О-2	Трубопровод системы подачи окислителя	-	-	-	Жидкий окислитель
О-3	Трубопровод системы подачи горючего	-	-	-	Жидкое горючее
О-4	КА	Управляющий импульс силы		-	-	-
	Электромагнитный клапан окислителя	1.Потоянное электрическое напряжение 2. Жидкий окислитель	О-1 О-2	Связь-прерывание	1.Жидкоий окислитель 2.Отсутствие жидкого окислит.
	Электромагнитный клапан окислителя	1.Потоянное электрическое напряжение 2. Жидкое горючее	О-1 О-3	Связь-прерывание	1.Жидкое горючее 2.Отсутствие жидкого горючего
	Камера	1.Жидкий окислитель 2.Жидкое горючее		Смешение, преобразование	1.Управляющий импульс силы КС 2.Продукты сгорания 3.Тепловая энергия 4.Давление рабочего тела	О-4
	Сигнализатор давления	1.Постоян. эл. напряжение 2.Давление рабочего тела		Связь-прерывание	1.Постоянный эл. сигнал 2.Отсутствие эл. напряжения	О-4

а) конкретизированная ФС

б) абстрагированная ФС

§6.7. Анализ и описание физического принципа действия (ФПД).

§6.8. Синтез ФПД по заданной физической операции.

§6.9. Автоматизированный синтез ФПД.

Тема 7. Моделирование – способ познания

§ 7.1. Понятие модели.

Слово модель происходит от латинского modulus – образец. В современном понимании с термином «модель» связан практически необозримый круг материальных и идеальных объектов – от одежды и обуви до дифференциальных уравнений и вычислительных алгоритмов.

Круг объектов, обозначаемых этим словом, настолько широк и разнороден, что невольно возникает мысль, что общего понятия модели не существует.

Опровержений этому сомнению есть несколько, например, «лингвистическое». Язык представляет собой настолько совершенную самоорганизующуюся систему, что случайное присвоение одного и того же имени сотням различных объектов, не имеющих между собой ничего общего, совершенно невероятно. Т.е. в этих объектах должно быть нечто общее, присущее всем. Чтобы выделить это общее, зайдём к вопросу с другой стороны.

Понятие модели неразрывно связано с новым знанием, с познанием. Познание – одно из основных занятий и предназначение человечества.

Фраза «человек познаёт мир» имеет несколько аспектов.

1 аспект. Младенец не имеет никакого практического опыта, и ему надо сначала научиться видеть, слышать, осязать, т.е. научиться сопоставлять ощущаемые объекты с некоторыми образами, возникающими в мозгу.

2 аспект. Во время получения образования в детском саду, школе, ВУЗе человек постигает то, что уже открыто до него другими. Изложение любого знания происходит в русле присущей этому материалу методики изложения и понимания. (Резерфорд).

Конечно, изучить всё, что уже открыто человечеством, невозможно одному человеку. Но некоторые люди достигают в определённых отраслях знания полного постижения и выходят к рубежу между уже известным и ещё неизвестным человечеству. Тогда у него есть возможность сделать «шаг за горизонт».

3 аспект. Познание чего-то такого, для чего ещё не существует формализованных методик изучения.

Цель любого познания – добиться понимания и контроля над некоторой частью вселенной. Процесс познания сложен, и это происходит потому, что сложен, многообразен мир, который мы познаём, сложен и многообразен в любом его проявлении.

«Что такое так называемая узкая проблема? Вот, возьмём только что упавшее яблоко. Почему упало именно это яблоко? Почему именно в данный момент? Механика соприкосновения яблока с землёй. Процесс передачи импульса. Условие обращённого падения. Квантовая картина падения. (Стругацкие)»

Ни одна часть Вселенной не является настолько простой, чтобы её можно было понять и управлять ею без абстракции. Абстракция – это замена рассматриваемой части Вселенной некоторой её моделью, имеющей схожую, но более простую структуру.

Что же такое модель? Понятие очень широко и может быть определено только в контексте оригинала и только в контексте задачи познания, решаемой субъектом. Т.е. если существует некоторая модель, значит, существует её оригинал и поставлена некоторая задача, связанная с оригиналом.

Определение. Модель в общем смысле есть создаваемый с целью получения или хранения информации специфический объект, отражающий свойства и связи объекта – оригинала, существенные для задачи, решаемой субъектом.

Т.е., упрощай, чтобы понимать.

Модели могут быть представлены в форме мысленного образа, описания знаковыми средствами либо материальной системой.

Преимущества модели перед оригиналом: доступность, обозримые в пространстве и времени масштабы, наглядность, эвристичность, неограниченные возможности для исследования и т.д.

Резюме.

1. Каждый материальный объект бесконечномерен. Полностью, в абсолютном смысле он может быть характеризован лишь бесконечным множеством признаков, свойств, характеристик.

2. Наши знания о материальном мире и входящих в его состав объектах на каждом этапе своего развития относительны и конечны; каждый реальный объект обладает рядом ещё непознанных признаков, свойств, характеристик.

3. Непосредственным результатом познавательного процесса, связанного с любым объектом материального мира, является формирование в сознании познающего субъекта идеального образа, который объективно отражает некоторые присущие объекту черты, свойства, характеристики. В формировании этого образа наряду с непосредственным восприятием активно участвуют теоретические представления, ранее накопленный опыт и вообще весь багаж знаний и практических навыков, которыми располагает субъект.

4. Познавательный процесс носит целенаправленный характер. В его основе во всех без исключения случаях лежит некоторая задача, которую решает субъект для достижения своих (не обязательно осознанных) целей.

5. Наивысшая эффективность любой модели достигается как разумный компромисс между близостью модели к оригиналу и простотой, обеспечивающей удобство использования модели по её прямому назначению.

§ 7.2. Классификация моделей

Чтобы лучше постичь понятие, которое является настолько общим, что не может быть определено через другие, более общие понятия, обычно прибегают к помощи примеров и исследуют свойства этого объекта. Для этих целей и призвана классификация моделей. Классификаций может быть много, более удачных и менее.

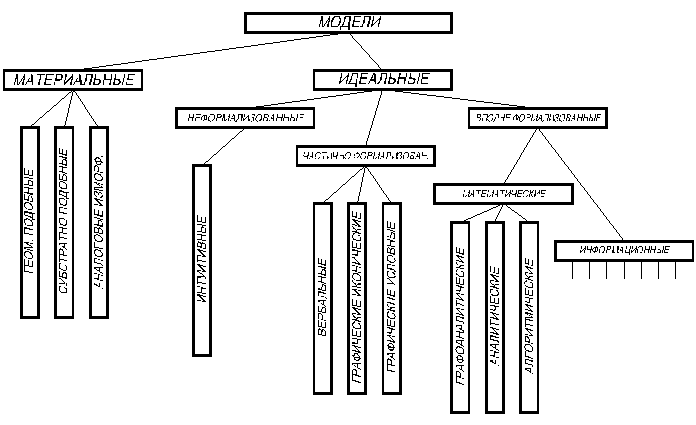
В приведённой классификации каждая модель характеризуется тремя основными признаками: принадлежностью к определённому классу задач, указанием типа объекта моделирования и способа реализации.

По классу задач.

Эстетические – относятся к сфере искусства.

Классы познавательных, планово-экономических, технологических задач: каждый обладает сложной структурой и может быть разделён на множество подклассов.

Кибернетические. Кибернетика представляет собой общую теорию информационных процессов управления и гомеостаза. Поэтому под кибернетической моделью надо понимать указание на принадлежность задачи к сфере исследования процессов управления и гомеостаза.

По классу объектов.

Классы объектов моделирования многочисленны и представлены на схеме лишь выборкой, достаточно случайной. Их номенклатура соответствует исторически сложившимся в науке и практике представлениям. Здесь также каждый класс имеет сложную структуру и может быть разделён на подклассы.

По форме представления информации модели подразделяются на материальные и идеальные, которые могут быть концептуальными, т.е. модели – представления, и знаковыми, базирующимися на некотором языке описания.

Материальные модели:

1) геометрически подобные масштабные (макеты, муляжи и т.д.)

2) субстратно подобные, воспроизводящие с масштабом в пространстве и времени свойства и характеристики оригинала той же природы, что и модель (гидродинамические модели судов, продувочные модели ЛА и др.)

3) аналоговые изоморфные, воспроизводящие исследуемые свойства и характеристики объекта-оригинала в моделирующем объекте иной природы на основе некоторой системы прямых аналогий (силу тяжести в космическом корабле, находящемся на геостационарной орбите, можно промоделировать центрифугой).

Идеальные модели.

1) Неформализованные. К ним относится единственный подкласс – концептуальные, модели – понятия. Это система представлений об объекте – оригинале, сложившаяся в человеческом мозгу.

2) Частично формализованные. Общим у них является использование языков, допускающих в некоторых пределах неоднозначность описаний.

- Вербальные модели. Описание свойств и характеристик оригинала на естественном языке.

Например, естественный язык. Асимметричный дуализм языкового знака. Белое безмозглое. Чаща всего.

- Графико-иконические модели – средствами графики представляют черты, свойства и характеристики оригинала, реально или хотя бы гипотетически доступные непосредственному зрительному восприятию (живопись, художественная графика, географические карты, чертежи и др.).

- Графические условные. Воспроизводят средствами графики свойства и характеристики объекта-оригинала, которые в принципе не могут наблюдаться визуально. Это всевозможные графики, диаграммы, схемы, обобщающие данные наблюдений и экспериментальных исследований. Объектами этих графических моделей могут являться:

а) объекты и величины реальные, но недоступные человеческому восприятию (например, магнитная индукция, уровень проникающей радиации);

б) искусственные, сконструированные на основе косвенных измерений величины (энтропия, энтальпия, температура).

Модели этого типа и для построения и для понимания требуют определённого уровня специальных знаний, образующих специфический язык данного типа моделей. Однако для специалиста, владеющего таким языком, наглядность и эвристичность этих моделей неоспорима.

3) Вполне формализованные модели. Общим признаком их являются во-первых, абстрактный характер всех компонент модели, которые представляют собой формально описанные элементы некоторого жёсткого языка, не допускающего многозначности толкования, а во-вторых, однозначное описание операций, которые допустимы над этими элементами. Также обязательным признаком таких моделей является то, что после формализации модель оказывается включённой в сферу применения логико-математических методов, и к ним может быть применён весь арсенал теоретической и вычислительной математики. Результаты анализа нуждаются в интерпретации, обратном переводе в термины и понятия исходной задачи.

Графо-аналитические. Это всевозможные геометрические интерпретации аналитических зависимостей, все разновидности графов, блок-схемы, в которых структура системы задаётся графически, а свойства компонентов описываются аналитически или алгоритмически.

Аналитические. Все виды функциональных зависимостей, алгебраические, дифференциальные и интегродифференциальные уравнения, векторы и векторные пространства, матричные формы, тензоры и т.д.

Алгоритмические (численные). Получаются в результате преобразования из аналитических форм, либо синтезируются непосредственно. Это наиболее универсальное средство математического моделирования.

Информационные. При использовании этих моделей объект-оригинал заменяется набором своих признаков. Информационные модели многочисленны и разнообразны. Как по характеру задач (ИПС, базы данных, АСУ и др.), так и с точки зрения используемых языков (ЛИСП, Симула, С++, Clsrion, Delphi и др.) Общая их особенность: относительно несложные алгоритмы, которые осуществляются над очень большими массивами данных. Все информационные модели узко специализированы.

Эвристико-алгоритмические имитационные. Использование математических моделей ограничено, т.к. объект-оригинал должен подвергаться математическому описанию, т.е. должен быть хорошо изучен. Также построение математической модели не даёт гарантии нахождения решения даже численными методами, т.к. существуют алгоритмически неразрешимые задачи. Реальный путь решения – органическое объединение эвристических способностей, ассоциативного мышления, творческих возможностей человеческого мозга с вычислительными возможностями ЭВМ. Это объединение реализуется в диалоговых человеко – машинных системах.

Дата добавления: 2014-01-13