Система сходящихся сил имеет равнодействующую, которая равна векторной сумме всех сил системы и приложена в точке пересечения их линий действия

И условия уравновешенности

Сходящимися называют силы, линии действия которых пересекаются в одной точке О (рис.6).

Пусть { F ₁, …, F _n } система сходящихся сил. Используя результат примера 1, переносим все силы в точку О. Затем, используя аксиому 3, находим их равнодействующую R как векторную сумму:

Рис.6

R = F ₁ + F ₂ +... + F _n =

В случае, когда равнодействующая равно нулю

R = F ₁ + F ₂ +... + F _n = 0, (1.1)

система { F ₁, …, F _n } эквивалентна «пустой» системе сил, а значит - является уравновешенной.

Очевидно, справедливо и обратное утверждение: для уравновешенной системы сходящихся сил { F ₁, …, F _n } ≡ 0 выполняется равенство (1.1). В противном случае равнодействующая R системы { F ₁, …, F _n } не равна нулю, а значит сама эта система не является уравновешенной.

Таким образом, система сходящихся сил является уравновешенной тогда и только тогда, когда векторная сумма всех её сил равна нулю

= 0 (1.2)

Для выполнения расчетов (решения задач) приходится использовать не векторную (1.2), а скалярную форму условия уравновешенности.

Как известно из векторной алгебры векторное равенство (1.2) равносильно трем скалярным:

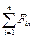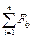= = = 0, (1.3)

где F_ix, F_iy, F_iz - проекции силы F _i на декартовы оси Ох, Оy, Oz.

Т.е. для уравновешенности системы сходящихся сил необходимо и достаточно, чтобы были равны нулю суммы их проекций на каждую из декартовых координатных осей.

Замечание 1. Вместо декартовых осей в (1.3) можно использовать любую тройку некомпланарных осей.

Замечание 2. Если силы лежат в одной плоскости, т.е. { F ₁, …, F _n } - плоская система сходящихся сил, то число необходимых и достаточных условий уравновешенности сокращается до двух:

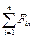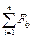= = 0, (1.4)

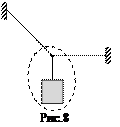
Пример 3. Найти натяжения тросов АВ и АС, удерживающих груз весом 600 Н (рис.7).

Для решения задачи рассмотрим равновесие той части композиции, которая обведена штриховой линией на рис.8.

На эту выделенную часть действуют сила тяжести Q груза, а также силы натяжения T ₁ и T ₂ тросов как показано на рис.9. Это сходящиеся силы, т.к. их линии действия пересекаются в точке А.

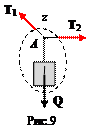
Воспользуемся условиями уравновешенности (1.4) плоской системы сходящихся сил. Для этого выберем оси Ах и Ay как показано на рис.10 и составим уравнения проекций (1.4):

,

.

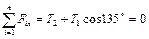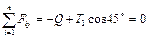Решая полученные уравнения, находим величины сил натяжения тросов. Из второго уравнения 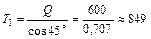Н, а из первого Н.

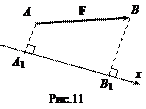Приложение 1. Вычисление проекции вектора на ось.

Пусть F - вектор, а x - ось произвольного направления. Из начала А и конца В вектора F опустим перпендикуляры на ось x и обозначим их основания А ₁ и В ₁ соответственно (рис.11).

Определение. Проекция вектора F на ось x – это число F_x, равное длине отрезка А ₁ В ₁, взятой со знаком + (плюс), если направление от А ₁ к В ₁ совпадает с направлением оси x и со знаком – (минус) в противном случае, т.е.

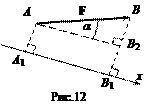F_x = ± А ₁ В ₁

Проведем из начала А вектора F прямую AВ ₂ параллельную оси x (рис.12). Обозначив a - угол между положительным направлением оси x и вектором F, получаем из прямоугольного треугольника АВ ₂ В:

F_x = ± А ₁ В ₁ = ± AВ ₂ = АВ cos a = F cos a,

где F = | F | = АВ - модуль (длина) вектора F.

Заметим, что полученная выше формула

F_x = F cos a (1.5)

Рис.13

будет справедливой при произвольном взаимном расположении вектора F и оси x. Так, если угол a тупой (рис.13), то cos a < 0 и, следовательно, F_x < 0, что полностью соответствует определению проекции.

Для некоторых частных случаев расположения вектора силы и оси вычисление проекций показано на рис.14.

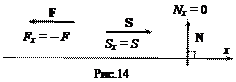
Приложение. Основные виды связей и их реакции

1. Гладкая поверхность. Если тело опирается на гладкую поверхность, то реакция направляется по нормали к этой поверхности (рис.15).

2. Гибкая невесомая нить. Если тело подвешено на гибкой невесомой нити, то реакция направляется вдоль нити в направлении от тела (рис.16).

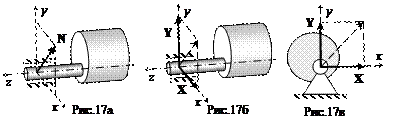
4. Цилиндрический шарнир. Если тело закреплено на цилиндрическом шарнире с осью вращения Оz, то реакция N направляется перпендикулярно оси Оz шарнира (рис.17а). Обычно, для удобства вычисления проекций и моментов такую реакцию разлагают на две составляющие X и Y, направленные вдоль соответствующих координатных осей (рис.17б). Условное обозначение цилиндрического шарнира на плоской расчетной схеме показано на рис.17в.

5. Подвижный шарнир. Так называют цилиндрический шарнир, ось которого имеет возможность перемещаться по заданной опорной плоскости (рис.18). Реакция подвижного шарнира направляется перпендикулярно этой плоскости (рис.18)

3. Невесомый стержень. Если тело опирается на невесомый стержень, то реакция направляется вдоль этого стержня (рис.19).

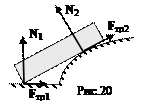6. Шероховатая поверхность. Реакция шероховатой поверхности кроме нормальной составляющей N (см.рис.15) включает в себя и касательную – силу трения F _тр (рис.20). Для силы трения выполняется неравенство

, (1.6)

где m - коэффициент трения скольжения, который зависит от материалов и качества обработки поверхностей соприкасающихся тел.

Задания для самостоятельной работы.

1. Какие из аксиом 1- 4 справедливы только для сил приложенных к абсолютно твердому телу?

2. Получите правило сложения двух параллельных одинаково направленных сил F ₁ и F ₂ , если их величины связаны соотношением а) F ₂ = 3 F ₁; б) F ₂ = l F ₁, где l - любое положительное число.

Указание. Можно воспользоваться приёмом, который продемонстрирован в примере 2.

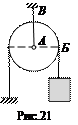3. Груз весом 800 Н подвешен на нити, перекинутой через блок Б (рис.21). Блок висит на нити АВ.

Укажите силы действующие на блок.

Является ли система сил, действующих на блок сходящейся?

Найдите натяжение нити АВ, на которой висит блок.

Дата добавления: 2014-01-13